Next: Calculating the Kinetic Energy Up: Classical Mechanics 110B Previous: Homework Problems Contents
In this chapter we will consider the motion of solid objects under the application of forces and torques. We call these solid objects ``Rigid Bodies''. Of course nothing is completely rigid. Objects deform elastically, but these deformation are negligible for a wide range of problems.
For a rigid body, we will find in the equations that the motion can be separated into the motion of the center of mass and the rotation around the center of mass.
In the rigid body limit, the state of a body can be described by six variables. These are the position of the center of mass and three angles to describe the orientation of the object.
We will apply some of the results we have derived for transformation from an inertial frame to a rotating frame. For now we choose the body to be at rest inside the rotating (body) frame and the origin to be at the center of mass.
For the purposes of calculation, we will assume that the body is made up of a set of discrete masses,
labeled by an index
![]() .
In any inertial frame, the velocity of one of those masses is
.
In any inertial frame, the velocity of one of those masses is
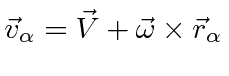
In introductory physics courses, we have learned about the moment of inertia and found that rotational
motion is analogous to simple kinetics,
with the analog of momentum
 being angular momentum
being angular momentum
![]() and
the analog of the kinetic energy equation
and
the analog of the kinetic energy equation
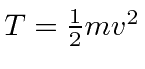 being
being
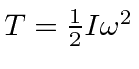 .
Thinking about the
rotational physics of a dumbbell, we can see that rotational motion is not always so simple.
Think about rotation of a dumb-ell about an axis at an angle
.
Thinking about the
rotational physics of a dumbbell, we can see that rotational motion is not always so simple.
Think about rotation of a dumb-ell about an axis at an angle
![]() to the axis.
We find that the angular momentum is always perpendicular to the axis and thus
to the axis.
We find that the angular momentum is always perpendicular to the axis and thus
![]() is not parallel to
is not parallel to
![]() .
.
Charles Stark Draper is shown below with a gyroscope used for the inertial guidance systems.
