Next: Lagrange Equations for Top Up: Dynamics of Rigid Bodies Previous: Example: Symmetric Top with Contents
Consider a general rigid body with
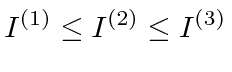 , rotating about one of the principal axes.
If small rotations about the other principal axes are introduced, will the rotation be stable?
(What happens if you toss a book in the air?)
, rotating about one of the principal axes.
If small rotations about the other principal axes are introduced, will the rotation be stable?
(What happens if you toss a book in the air?)
Lets start with rotations about the first principal axis with the smallest moment of inertia.
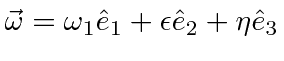
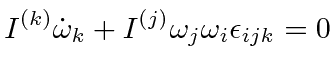 |
||
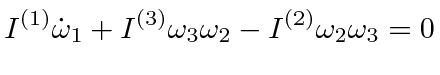 |
||
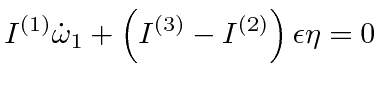 |
||
 |
||
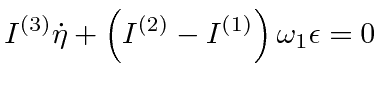 |
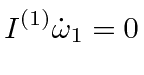 |
||
 |
||
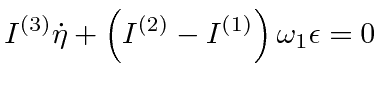 |
||
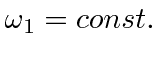 |
||
 |
||
 |
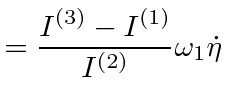 |
||
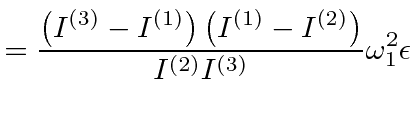 |
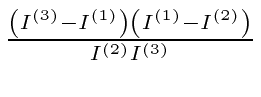 is negative, the solutions are oscillatory.
If it is positive, they can grow exponentially.
The constant is negative for axis 1.
(Note that the
is negative, the solutions are oscillatory.
If it is positive, they can grow exponentially.
The constant is negative for axis 1.
(Note that the
The
equation can actually be applied to any of the three axes.
For axis 2, the constant is
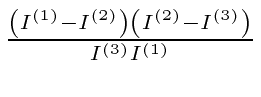 which is positive,
and the oscillations are unstable.
For axis 3, the constant is
which is positive,
and the oscillations are unstable.
For axis 3, the constant is
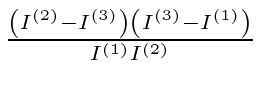 which is negative
and the oscillations are stable.
which is negative
and the oscillations are stable.
So rotations about the axes with the lowest and highest moment are stable while oscillations about the axis with the intermediate moment are unstable. Try it with a book.
Jim Branson 2012-10-21