Next: Stability of Rigid Body Up: Euler's Equations Previous: Euler's Equations Contents
The primary application of this equation is motion with no torque since its hard to transform a torque into the body frame.
We now consider a
symmetric top, that is an object with
![]() .
The equations are.
.
The equations are.
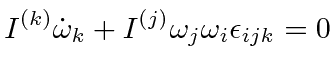 |
||
 |
||
 |
||
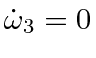 |
||
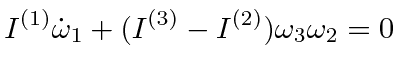 |
||
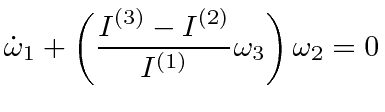 |
||
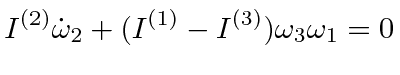 |
||
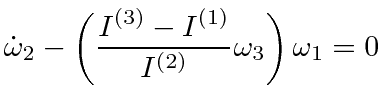 |
||
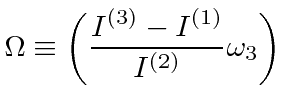 |
||
 |
||
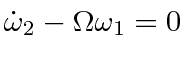 |

Since there is no torque,
![]() is constant in the inertial system.
The angle between
is constant in the inertial system.
The angle between
![]() and
and
![]() is constant in the inertial system,
since
is constant in the inertial system,
since
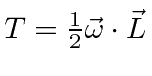 is constant and the magnitude of
is constant and the magnitude of
![]() is constant.
So
is constant.
So
![]() precesses around
precesses around
![]() in the fixed system.
We can choose
in the fixed system.
We can choose
![]() along
along
![]() since it is constant.
We can show that
since it is constant.
We can show that
![]() ,
,
![]() , and
, and
![]() are in a plane.
This can be shown by computing
are in a plane.
This can be shown by computing
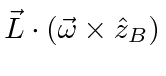 and showing it is zero.
and showing it is zero.
The rate of precession is
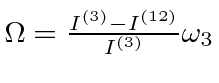 .
This is small if the moments of inertia are nearly the same.
Examples of this effect are Frisbees wobbling, a spiral pass in football, and maybe the oblate earth's precession.
(The dominant term for the earth is gravity driven so we need to analyze it with an external torque.)
.
This is small if the moments of inertia are nearly the same.
Examples of this effect are Frisbees wobbling, a spiral pass in football, and maybe the oblate earth's precession.
(The dominant term for the earth is gravity driven so we need to analyze it with an external torque.)
Jim Branson 2012-10-21