Euler's Equations

It is simple to derive a set of equations describing the motion of a rotating object in the rotating (Body) frame. If an external torque is applied, it may be difficult to work in the body system so this will most often be useful for problems with no torque.

In the Inertial system, we have

$$\dot{\vec{L}}_{inertial}=\vec{\Gamma}$$

where $\vec{\Gamma}$ is the applied torque. This time derivative can be transferred to the body system using the equation

$$\left({d\vec{L}\over dt}\right)_{inertial}=\left({d\vec{L}\over dt}\right)_{rotating} + \vec{\omega}\times\vec{L}$$

which we will equate to the torque to get.

$${d\vec{L}_B\over dt} + \vec{\omega}\times\vec{L} = \vec{\Gamma}$$

$$\dot{L}_{Bk} + \omega_iL_j\epsilon_{ijk} = \Gamma_k$$

$$L_{Bk}=I^{(k)}\omega_k$$

$$\dot{L}_{Bk}=I^{(k)}\dot{\omega}_k$$

$$I^{(k)}\dot{\omega}_k + \omega_iI^{(j)}\omega_j\epsilon_{ijk} = \Gamma_k$$

These are the Euler Equations.

$$I^{(k)}\dot{\omega}_k + I^{(j)}\omega_j\omega_i\epsilon_{ijk} = \Gamma_k$$

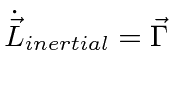
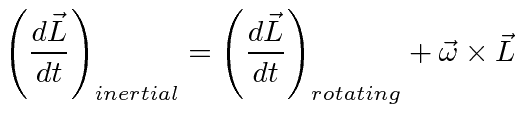
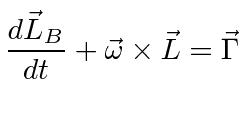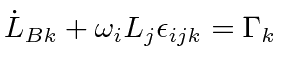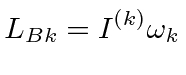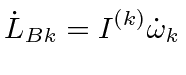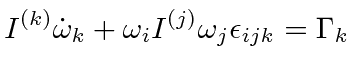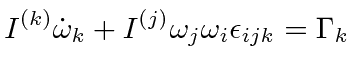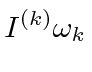Note that we have used the notation $I^{(k)}$ with a superscript to make it clear that $I$ is not a vector but rather three numbers that go with the three principal axes so a combination like $I^{(k)}\omega_k$ does not imply a sum over $k$