Body Frame Coordinates

A constant rotation about an axis written in the Body system is made up of the three rotations.

$$\vec{\omega}=\dot{\phi}\hat{z}_I+\dot{\theta}\hat{x}'+\dot{\psi}\hat{z}_B$$

We can get the first one from the rotation matrix we just calculated.

$$\hat{z}_{Ii}=R_{ij}\delta_{j3}=R_{i3}=(\sin\theta\sin\psi,\sin\theta\cos\psi,\cos\theta)$$

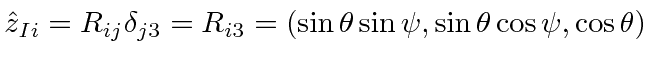
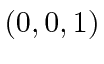The $\psi$ rotation is about the $z_B$ axis in the Body system so its just $(0,0,1)$. The unit vector for the $\theta$ rotation can be calculated from the $\psi$ rotation matrix.

$$\hat{x}'_i=R_{i1}(\psi)=(\cos\psi,-\sin\psi,0)$$

Putting this together, we get the $\vec{\omega}$ corresponding to the derivatives of the Euler angles.

$$\vec{\omega}=(\dot{\phi}\sin\theta\sin\psi+\... ...sin\theta\cos\psi-\dot{\theta}\sin\psi, \dot{\phi}\cos\theta+\dot{\psi})$$

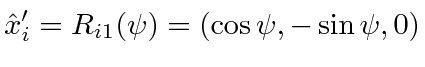
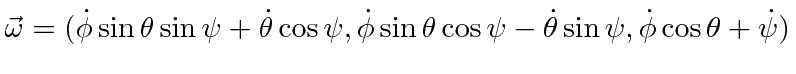Euler angles may be useful to describe the motion of a rotating object. The description is in the Body system where it is easy to work with the Inertia tensor, but hard to deal with external torque that is given in the Inertial system. Some problems can be solved without using the Euler Angles but they are useful for many problems.

The dynamics of rotating objects can be fairly complicated so it is useful to pick the body coordinate system to make the problem as simple as possible. The origin of the body coordinate system will be at the center of mass. The axes of the body coordinate system will be the principal axes of the object. These axes are rotating with the object.