Next: Body Frame Coordinates Up: Dynamics of Rigid Bodies Previous: Proof: Roots are Real Contents
Three angles are needed to describe an arbitrary rotation.
There are an infinite number of ways to do this but the
Euler angles are most often used.
This is a slightly complicated problem, no matter how you define the angles.
We will go
from the Inertial system to the Body system,
in three steps from
![]() to
to
![]() to
to
![]() to
to
![]() .
.
The three steps are
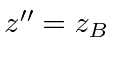 axis.
axis.
The three rotations are shown in the figure below.
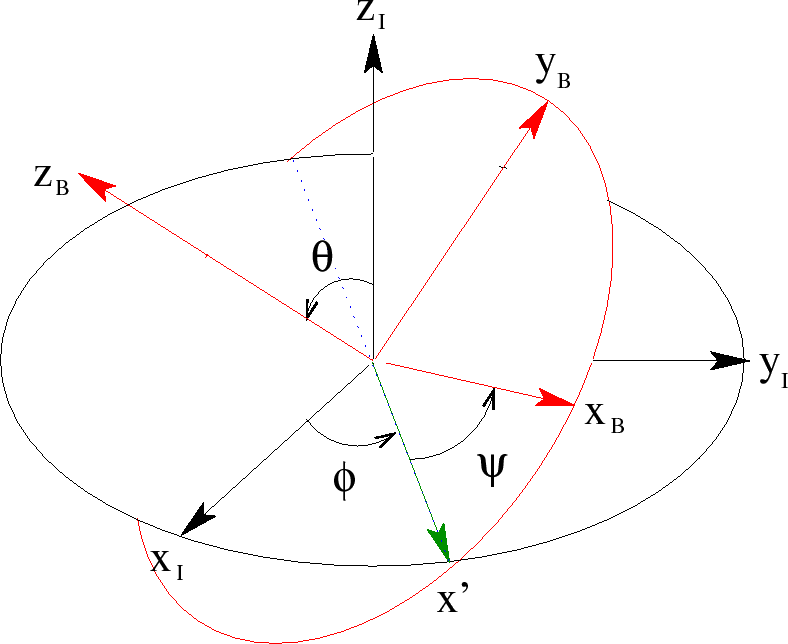
The resulting rotation matrix
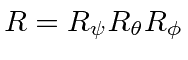 can be straightforwardly calculated.
can be straightforwardly calculated.
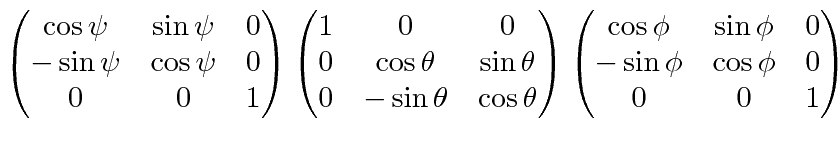 |
|
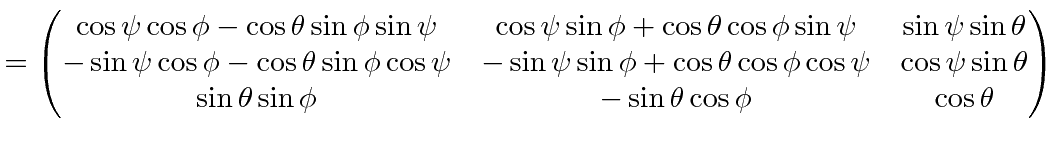 |
|
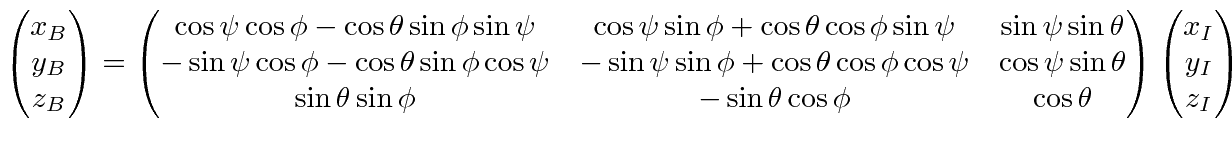 |

Jim Branson 2012-10-21