Next: Homework Up: Dynamics of Rigid Bodies Previous: Stability of Rigid Body Contents
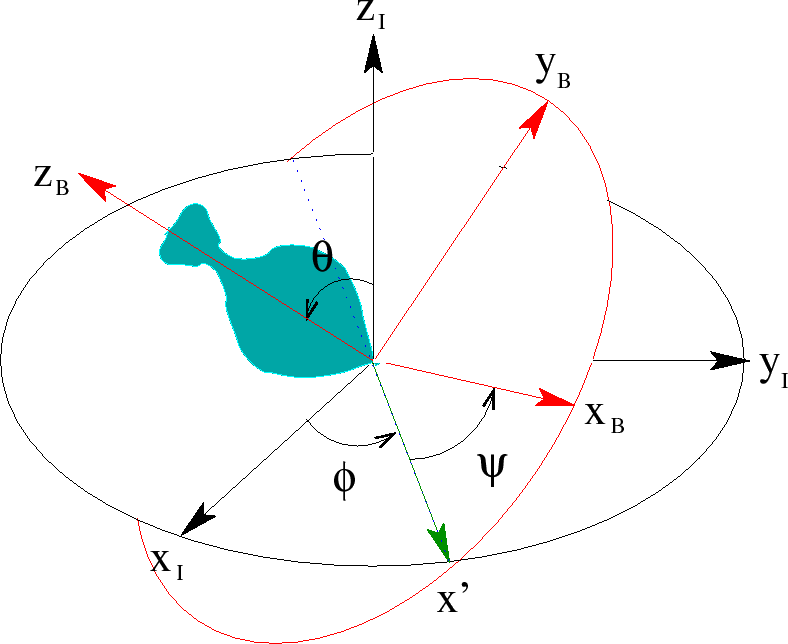
We can analyze the motion of a spinning top using the Lagrange equations for the Euler angles. Let us assume that the top has its lowest point (tip) fixed on a surface. We will use the fixed point as the origin. The rotation about the origin will be described by the Euler angles so that all the kinetic energy is contained in the rotation.
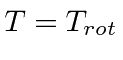

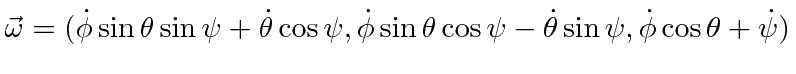
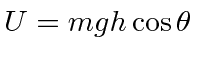
 |
||
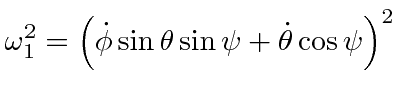 |
||
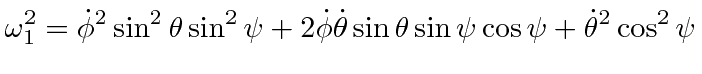 |
||
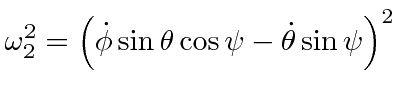 |
||
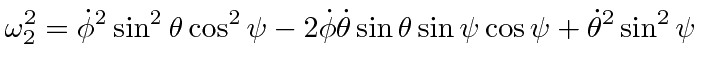 |
||
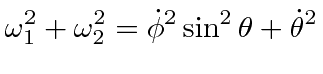 |
||
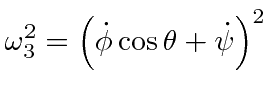 |
||
 |
||
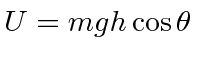 |
||
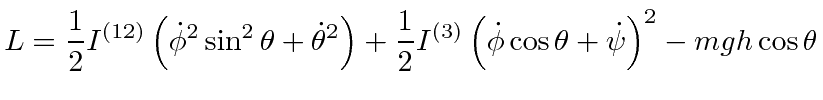 |
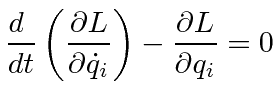
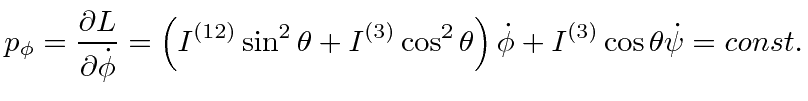
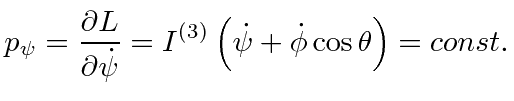
So
![]() and
and
![]() are constants of the motion and we can solve the equations for
are constants of the motion and we can solve the equations for
![]() and
and
![]() .
.
 |
||
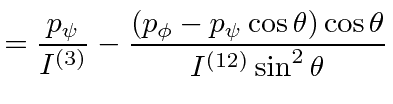 |
There is a third Lagrange equation but it will be easier to understand the motion of the top by using the total energy equation, along with the two conserved momenta.
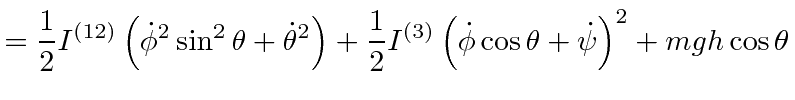 |
||
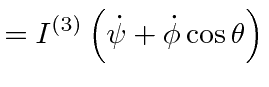 |
||
 |
||
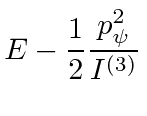 |
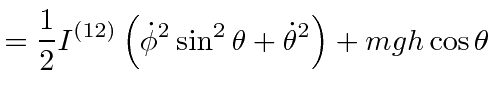 |
|
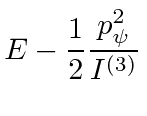 |
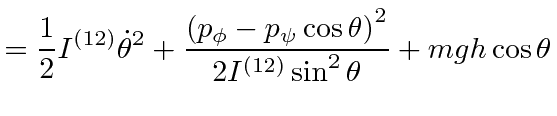 |
|
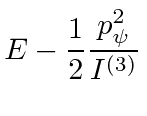 |
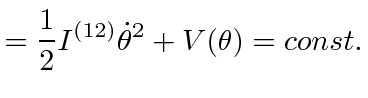 |
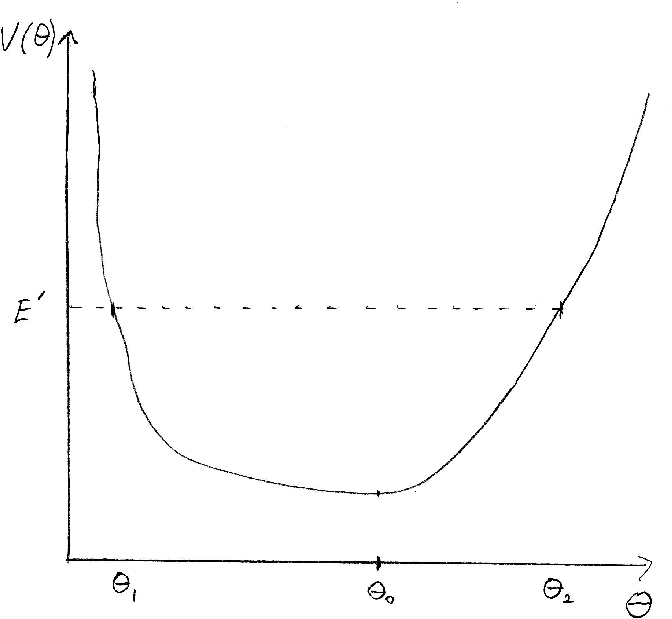
This is very much
like a central force problem with the mass oscillating back and forth in the potential.
![]() goes to zero at the limits.
The motion will be limited between the some angles
goes to zero at the limits.
The motion will be limited between the some angles
![]() and
and
![]() at which
at which
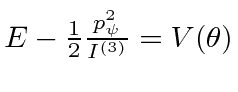 .
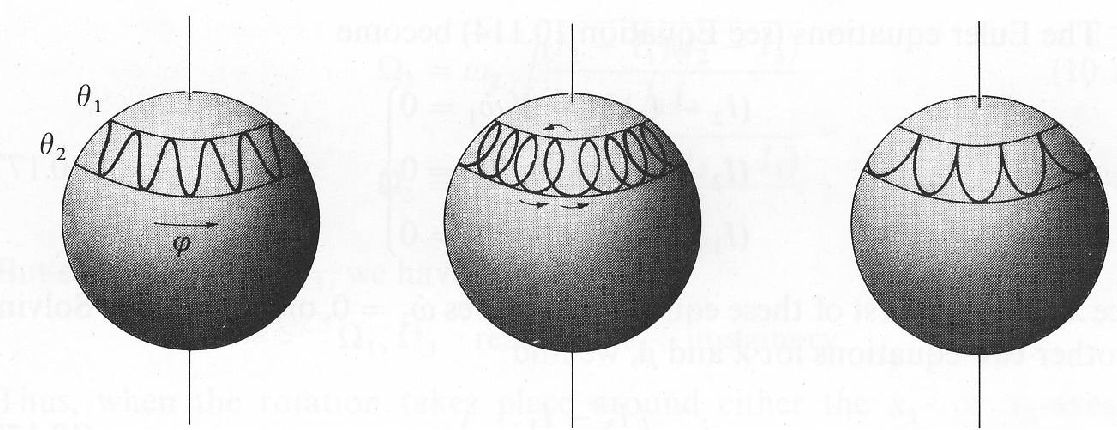
This oscillation of
.
This oscillation of
![]() as the angular momentum precesses is called
nutation.
as the angular momentum precesses is called
nutation.
Jim Branson 2012-10-21