- Calculate the three principal moments of inertia for a cone of mass
 , height
, height  , and radius at the base
, and radius at the base 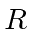 ,
using the cone's apex as the origin.
,
using the cone's apex as the origin.
- Transform the moments of inertia from the previous problem to an origin at the center of mass of the cone.
- Find the height at which a billiard ball should be struck so that is will roll with no initial slipping.
Find the optimum height for a rail on a billiard table.
- A homogeneous cube of side
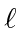 is balanced with one edge resting on a horizontal surface.
The cube is allowed to fall.
Show that the angular velocity of the cube
when one face hits the surface would be
is balanced with one edge resting on a horizontal surface.
The cube is allowed to fall.
Show that the angular velocity of the cube
when one face hits the surface would be
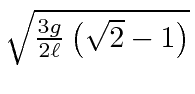 if the edge cannot slip on the surface.
What would be the angular velocity if the edge can move frictionlessly on the surface?
if the edge cannot slip on the surface.
What would be the angular velocity if the edge can move frictionlessly on the surface?
- A rigid body consists of three masses connected by nearly massless rods.
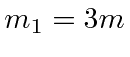 at
at 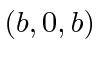
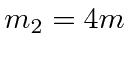 at
at 
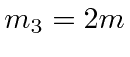 at
at 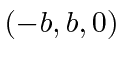
Find the inertia tensor for rotations about the given origin.
Find the principal moments of inertia (but don't bother to find the axes).
- What are the principal axes and principal moments of inertia of a uniform density solid hemisphere, about its center of mass.
Assume the hemisphere has a mass
 and radius
and radius 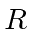 .
.
- Consider the inertia tensor
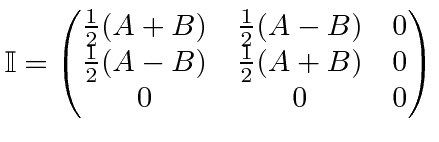 .
Perform a rotation about the
.
Perform a rotation about the 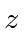 axis through an angle
axis through an angle 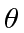 .
Show that a rotation for
.
Show that a rotation for
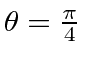 renders the tensor diagonal.
What are the principal moments of inertia.
renders the tensor diagonal.
What are the principal moments of inertia.
- Show that the trace of a tensor is invariant under rotations.
- A thin, uniform plate in the shape of an equilateral triangle hangs from the midpoint of one side.
Find the frequency of small (pendulum) oscillations.
- Show that for force-free and torque-free motion of a symmetric top, that the angular momentum, the angular velocity,
and the axis of symmetry lie in a plane.
- A symmetric top, with gravity acting on it, rotates about the vertical direction.
Assume the center of mass is a height
 above the table.
Calculate (and sketch) the effective potential as a function of
above the table.
Calculate (and sketch) the effective potential as a function of 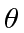 and find the condition on
and find the condition on 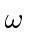 for the motion to be stable.
for the motion to be stable.
Jim Branson
2012-10-21
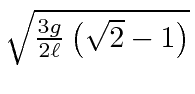 if the edge cannot slip on the surface.
What would be the angular velocity if the edge can move frictionlessly on the surface?
if the edge cannot slip on the surface.
What would be the angular velocity if the edge can move frictionlessly on the surface?
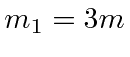 at
at 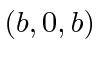
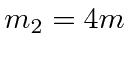 at
at 
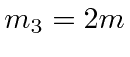 at
at 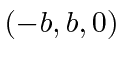
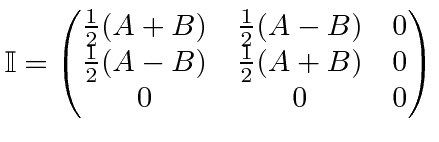 .
Perform a rotation about the
.
Perform a rotation about the 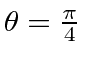 renders the tensor diagonal.
What are the principal moments of inertia.
renders the tensor diagonal.
What are the principal moments of inertia.