Angular Momentum

We may compute the angular momentum for a rigid body rotating about an axis going through its center of mass in the same way.

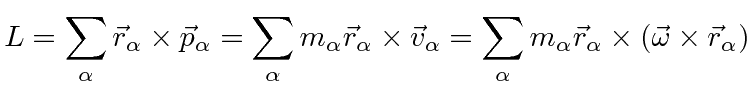
$\bgroup\color{black}$\displaystyle L=\sum\limits_\alpha\vec{r}_\alpha\times\vec{... ...\alpha\vec{r}_\alpha\times\left(\vec{\omega}\times\vec{r}_\alpha\right) $\egroup$

Now use the vector identity we computed earlier.

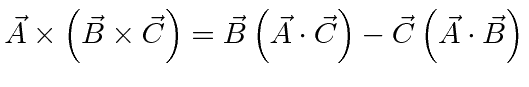
$\bgroup\color{black}$\displaystyle \vec{A}\times\left(\vec{B}\times\vec{C}\right... ...left(\vec{A}\cdot\vec{C}\right)-\vec{C}\left(\vec{A}\cdot\vec{B}\right) $\egroup$

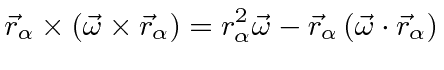
$\bgroup\color{black}$\displaystyle \vec{r}_\alpha\times\left(\vec{\omega}\times\... ...\vec{\omega}-\vec{r}_\alpha\left(\vec{\omega}\cdot\vec{r}_\alpha\right) $\egroup$

$\bgroup\color{black}$\displaystyle \vec{L}=\sum\limits_\alpha m_\alpha\left[r_\a... ...mega}-\vec{r}_\alpha\left(\vec{\omega}\cdot\vec{r}_\alpha\right)\right] $\egroup$

Now lets write this for the components of $\bgroup\color{black}$ \vec{L}$\egroup$ .

$\bgroup\color{black}$\displaystyle L_i=\sum\limits_\alpha m_\alpha\left[\omega_i... ...\delta_{ij} r_\alpha^2- r_{\alpha i}r_{\alpha j}\right] =I_{ij}\omega_j $\egroup$

The angular momentum can be written in terms of the same inertia tensor.

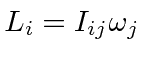$\bgroup\color{black}$ \displaystyle L_i =I_{ij}\omega_j$\egroup$

$\bgroup\color{black}$ \displaystyle \vec{L}=\mathbb{I}\vec{\omega}$\egroup$

Now we notice an important feature of rotations of rigid bodies. The angular moment will not be parallel to the angular velocity if the inertia tensor has off diagonal components.

Jim Branson 2012-10-21