Next: Transforming the Inertia Tensor Up: The Inertia Tensor Previous: Angular Momentum Contents
As a simple example of this phenomenon, consider two equal (point) masses
![]() , connected by a massless rod of length
, connected by a massless rod of length
![]() .
Assume it rotates about a fixed axis at an angle
.
Assume it rotates about a fixed axis at an angle
![]() to the rod.
First, note that since
to the rod.
First, note that since
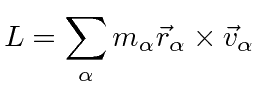
We might also note that if the dumbbell rotates about any axis perpendicular to the rod,
![]() is parallel to
is parallel to
![]() .
.
Now lets compute the inertia tensor in two coordinate systems.
Both should have the origin at the center of mass, in the middle of the rod.
First, with the rod in the
![]() plane at an angle
plane at an angle
![]() from the
from the
![]() axis.
Note that we are working in the rotating (body) frame in which the masses are at rest.
axis.
Note that we are working in the rotating (body) frame in which the masses are at rest.
![$\displaystyle I_{ij} \equiv \sum\limits_\alpha m_\alpha\left[\delta_{ij}r_\alpha^2-r_{\alpha i} r_{\alpha j}\right]$](img358.png) |
||
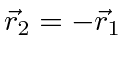 |
||
![$\displaystyle I_{ij} = 2m{\ell^2\over 4}\left[\delta_{ij}-\hat{r}_{i} \hat{r}_{j}\right]$](img360.png) |
||
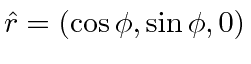 |
||
![$\displaystyle I_{11} = {m\ell^2\over 2}\left[1-\cos^2\phi\right]$](img362.png) |
||
![$\displaystyle I_{12} = I_{21} = {m\ell^2\over 2}\left[-\cos\phi\sin\phi\right]$](img363.png) |
||
![$\displaystyle I_{22} = {m\ell^2\over 2}\left[1-\sin^2\phi\right]$](img364.png) |
||
![$\displaystyle I_{33} = {m\ell^2\over 2}\left[1\right]$](img365.png) |
||
![$\displaystyle I_{31} = I_{13} = {m\ell^2\over 2}\left[0\right]$](img366.png) |
||
![$\displaystyle I_{23} = I_{32} = {m\ell^2\over 2}\left[0\right]$](img367.png) |
||
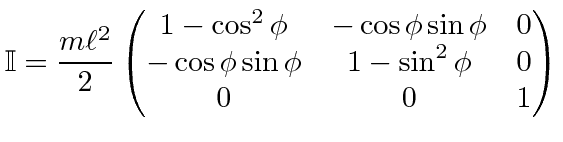 |
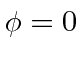 or
or
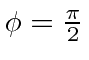 when the rod is along the
when the rod is along the
Jim Branson 2012-10-21