- Calculate the potential due to the earth's gravity plus the tidal force of the moon.
Use this to estimate the height of the high tide.
Now assume that not only the ocean moves due to the tidal force but that the land is floating on a fluid which
can deform due to the tidal force.
What would be the height of the tide if the land masses also respond to the tidal potential?
- A circular container of water rotates about its axis, which is vertical, with an angular frequency
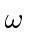 .
After some time, due to viscosity, the water becomes stationary in the rotating frame.
What is the shape of the water in the container (with normal gravity)?
.
After some time, due to viscosity, the water becomes stationary in the rotating frame.
What is the shape of the water in the container (with normal gravity)?
- A projectile is shot vertically (vertical determined by plumb bob) upward to a (small) height
 ,
at a northern latitude
,
at a northern latitude 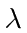 .
Show that it strikes the ground a distance of
.
Show that it strikes the ground a distance of
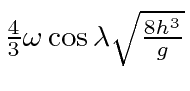 to the west of the point from which is was shot.
to the west of the point from which is was shot.
- A cannonball is fired due east with a velocity
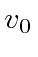 and inclination angle
and inclination angle 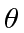 at a latitude
at a latitude 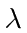 .
Show that the cannonball is deflected a distance
.
Show that the cannonball is deflected a distance
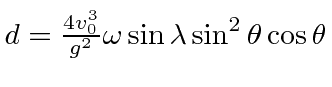 to the south.
to the south.
- A cannonball is fired due east with a velocity
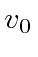 and inclination angle
and inclination angle 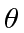 at a latitude
at a latitude 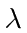 .
If the range of the cannonball is
.
If the range of the cannonball is 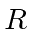 neglecting the rotation of the earth,
show that the range is increased by
neglecting the rotation of the earth,
show that the range is increased by
 .
.
- Show that the angular deviation of a plumb bob, from the direction toward the center of the earth, is
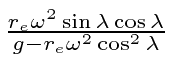 .
Find the maximum deviation in milleradians.
.
Find the maximum deviation in milleradians.
- Write the Lagrangian for a particle's motion in a potential
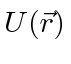 in an inertial coordinate system.
Now write the Lagrangian in a rotating coordinate system.
Finally calculate the Hamiltonian in the rotating frame and see if it is the total energy.
in an inertial coordinate system.
Now write the Lagrangian in a rotating coordinate system.
Finally calculate the Hamiltonian in the rotating frame and see if it is the total energy.
Jim Branson
2012-10-21
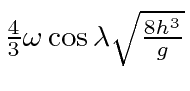 to the west of the point from which is was shot.
to the west of the point from which is was shot.
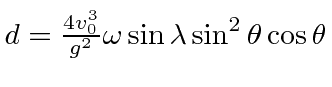 to the south.
to the south.
 .
.
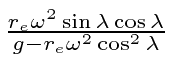 .
Find the maximum deviation in milleradians.
.
Find the maximum deviation in milleradians.
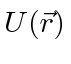 in an inertial coordinate system.
Now write the Lagrangian in a rotating coordinate system.
Finally calculate the Hamiltonian in the rotating frame and see if it is the total energy.
in an inertial coordinate system.
Now write the Lagrangian in a rotating coordinate system.
Finally calculate the Hamiltonian in the rotating frame and see if it is the total energy.