Next: Homework Problems Up: The Tides Previous: Weather Systems Contents
A heavy weight on a long cable is suspended from a mount that is free to swing in any direction with very small friction.
This is a Foucault pendulum.
Its equilibrium position is along the line of a plumb bob, in the direction of effective gravity.
With the long cable, the oscillations are small, so the velocity is horizontal
and we
do everything only to first order in
![]() .
.
Its natural to put the origin of coordinates at the equilibrium point, the z axis up, the y axis north, and the x axis east.
The motion is in the
![]() plane.
plane.
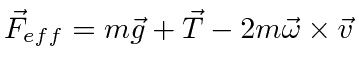 |
||
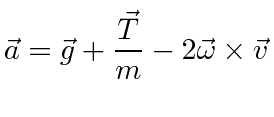 |
||
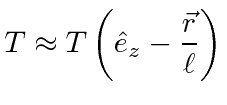 |
||
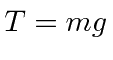 |
||
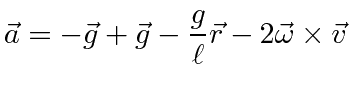 |
||
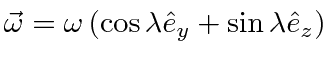 |
||
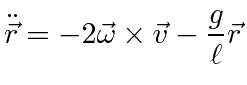 |
||
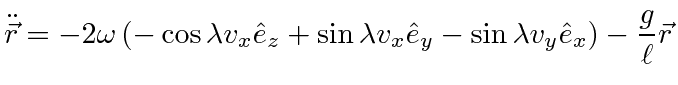 |
||
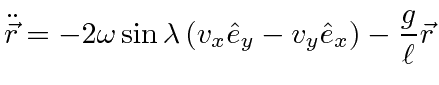 |
||
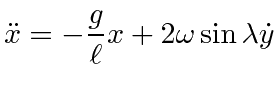 |
||
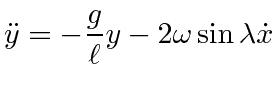 |
||
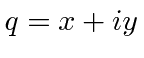 |
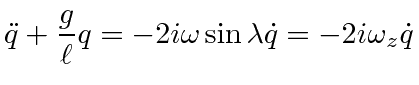 |
||
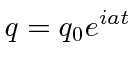 |
||
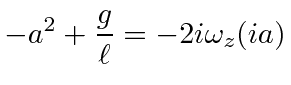 |
||
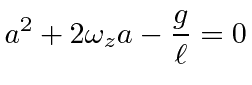 |
||
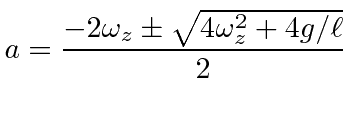 |
||
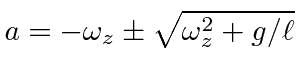 |
||
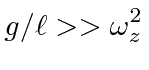 |
||
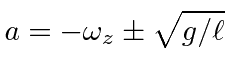 |
||
![$\displaystyle q(t)=q_0e^{-i\omega_z t}\left[A e^{i\sqrt{g/\ell}t} + B e^{-i\sqrt{g/\ell}t} \right]$](img299.png) |
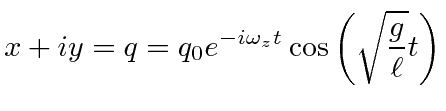 |
||
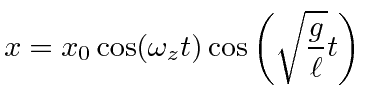 |
||
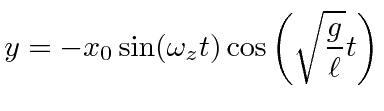 |
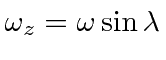 .
.
Jim Branson 2012-10-21