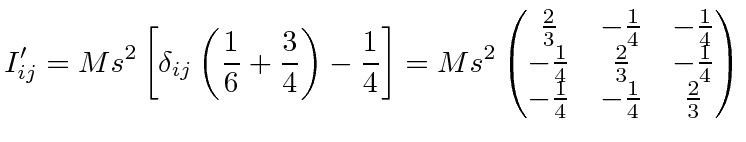We wish to compute the inertia tensor for a uniform density cube of mass
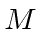 and side
and side
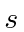 .
The density is simply
.
The density is simply
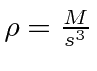 .
.
There are only two kinds of integrals. The rest are symmetric.
The inertia tensor is diagonal so rotation about these axes will have the angular momentum parallel to the axis.
The angular momentum then does not change with time and no torque is needed to rotate the cube.
Now lets consider
rotating a cube about one of its corners.
We can compute the new inertia tensor by using the parallel axis theorem with a translation of
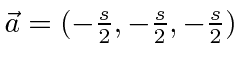 .
.
Note that the final
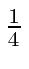 has no indices so it is subtracted from all 9 terms in the tensor.
has no indices so it is subtracted from all 9 terms in the tensor.
This inertia tensor is not diagonal so torque will be required to keep a cube rotating about a corner if the axis
of rotation in one of the edges of the cube.
(Note that angular momentum and torque are
measured relative to some origin so the location of the origin is important
in the calculation of the inertia tensor.)
For any
rotating mechanical part, it is important that it rotate about a
principal axis, otherwise it will exert torque
and cause vibrations.
Jim Branson
2012-10-21
![]() and side
and side
![]() .
The density is simply
.
The density is simply
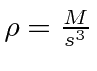 .
.
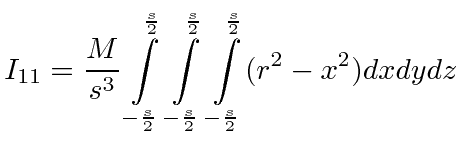
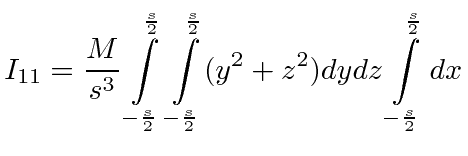

![$\displaystyle I_{11}={M\over 3s}(\left[y^3\right]_{-{s\over 2}}^{s\over 2}+\left[z^3\right]_{-{s\over 2}}^{s\over 2})$](img395.png)
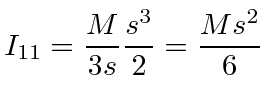
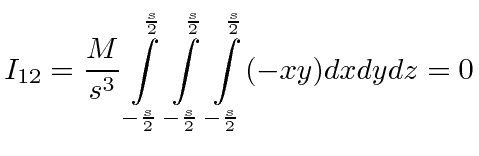
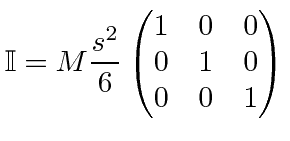
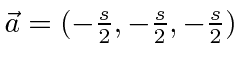 .
.
![\bgroup\color{black}$\displaystyle I_{ij}'=I_{ij}+M\left[\delta_{ij}a^2-a_ia_j\r...
...ver 4}\right]
=I_{ij}+Ms^2\left[\delta_{ij}{3\over 4}-{1\over 4}\right] $\egroup](img400.png)