Principal Axes

For any object (and origin), there is (at least one) a set of principal axes for which the inertia tensor is diagonal. It can be shown that he axes are orthogonal. Sometimes there is more than one set, particularly in cases of symmetry.

We can find the principal axes, or the axes of rotation that do not require torque by solving an eigenvalue equation. Basically we want to pick a direction for $\omega$ so that the angular momentum is parallel to $\omega$.

$$\mathbb{I}\vec{\omega}=I\vec{\omega}$$

$$I_{ij}\omega_j=I\omega_i$$

$$\left(I_{ij}-I\delta_{ij}\right)\omega_j = 0$$

For this to be zero, the determinant of the matrix has to be zero. Setting the determinant equal to zero we can find the eigenvalues $I$.

$$\left\vert\begin{matrix}I_{11}-I & I_{12} & I... ...22}-I & I_{23} \cr I_{31} & I_{32} & I_{33}-I \end{matrix}\right\vert=0$$

This yields a cubic equation giving three roots which are the eigenvalues for the three principal axes. Once we have the eigenvalues, we can solve the equation for the three axes or $\vec{\omega}$s that give the eigenvalues. The principal axes will be real and orthogonal.

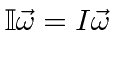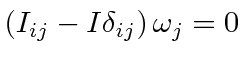The principal axes are real and orthogonal.

For a sphere, which has the highest symmetry, the three eigenvalues will be equal. For a symmetric top, two will be equal. For an asymmetric top, they will probably all be different.