Next: Proof: Roots are Real Up: Principal Axes Previous: Example: Cube Rotating about Contents
Take two principal axes
![]() and
and
![]() .
.
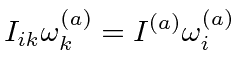 |
|
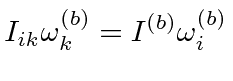 |
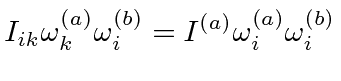 |
first eq. | |
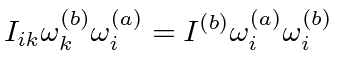 |
second eq. | |
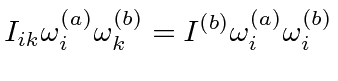 |
commute omegas | |
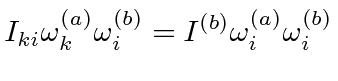 |
rename indices lhs | |
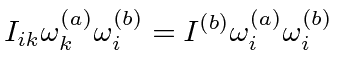 |
inerta tensor is symmetric |
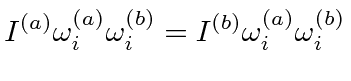 |
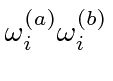 must be zero if the moments are not equal.
If they are equal, we can just choose orthogonal axes.
must be zero if the moments are not equal.
If they are equal, we can just choose orthogonal axes.
Jim Branson 2012-10-21