Next: Proof: Principal Axes Orthogonal Up: Principal Axes Previous: Principal Axes Contents
We have computed the inertia tensor for a cube with the origin at a corner and the axes along the edges.
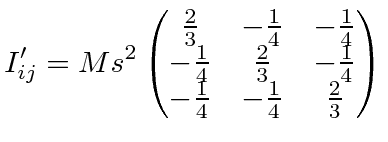
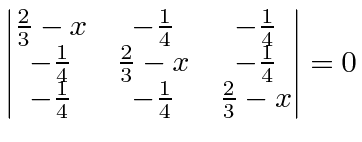
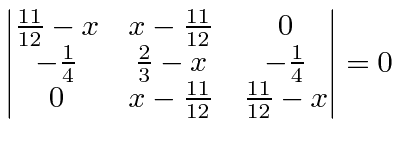
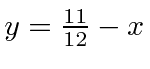 , we can write the determinant.
, we can write the determinant.
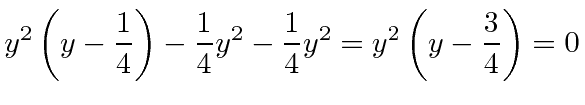
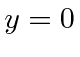 ,
,
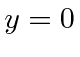 , and
, and
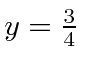 ; corresponding to three values for
; corresponding to three values for
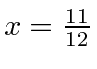 ,
,
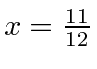 , and
, and
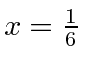 .
.
Knowing that two equal moments of inertia along principal axes indicate a symmetry, lets find the axis for the
third value
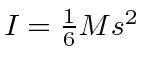 .
.
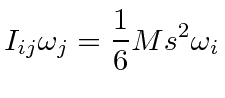 |
||
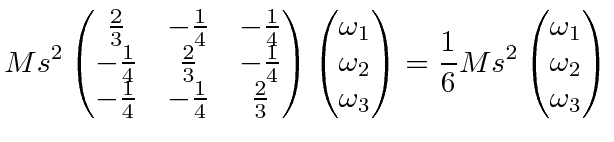 |
||
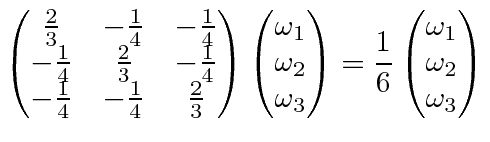 |
||
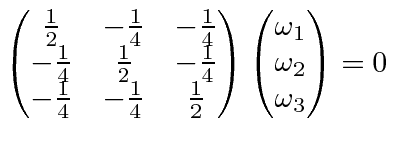 |
||
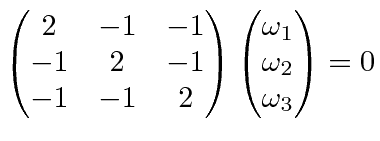 |
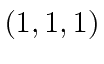 .
.
The other roots just give the same equation three times
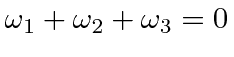 .
There are many possible solutions. The equation defines a plane perpendicular to the cube diagonal.
We can choose and orthogonal pair of axes in that plane.
.
There are many possible solutions. The equation defines a plane perpendicular to the cube diagonal.
We can choose and orthogonal pair of axes in that plane.
Jim Branson 2012-10-21