Next: Example: The Inertia Tensor Up: Dynamics of Rigid Bodies Previous: Transforming the Inertia Tensor Contents
If the inertia tensor for a set of axes with the center of mass at the origin is calculated, the tensor for any set of parallel axes can be easily derived. The translation of the coordinates is given by
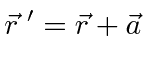
![$\displaystyle I_{ij} = \sum\limits_\alpha m_\alpha\left[\delta_{ij}r_\alpha^2-r_{\alpha i} r_{\alpha j}\right]$](img382.png) |
||
![$\displaystyle I_{ij}' = \sum\limits_\alpha m_\alpha\left[\delta_{ij}\left(\vec{r}_\alpha +\vec{a}\right)^2-(r_{\alpha i}+a_i)(r_{\alpha j}+a_j)\right]$](img383.png) |
||
![$\displaystyle I_{ij}'= \sum\limits_\alpha m_\alpha\left[\delta_{ij}\left(r_\alp...
...ight) -(r_{\alpha i}r_{\alpha j}+r_{\alpha i}a_j+a_ir_{\alpha j}+a_ia_j)\right]$](img384.png) |
||
![$\displaystyle I_{ij}'= I_{ij}+\sum\limits_\alpha m_\alpha\left[\delta_{ij}\left...
..._\alpha\cdot\vec{a}+a^2\right) -(r_{\alpha i}a_j+a_ir_{\alpha j}+a_ia_j)\right]$](img385.png) |
||
![$\displaystyle I_{ij}'= I_{ij}+\sum\limits_\alpha m_\alpha\left[\delta_{ij}\left(a^2\right)-(a_ia_j)\right]$](img386.png) |
||
![$\displaystyle I_{ij}'= I_{ij}+M\left[\delta_{ij}a^2-a_ia_j\right]$](img387.png) |
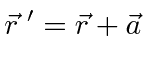 |
![\bgroup\color{black}$ \displaystyle I_{ij}'=I_{ij}+M\left[\delta_{ij}a^2-a_ia_j\right]$\egroup](img388.png) |
Note that the parallel axis theorem shows how the inertia tensor depends on the origin. Angular momentum, torque, and kinetic energy all depend on the origin. This is physically relevant if the origin is a fixed point in the rotation. The origin should be chosen to satisfy the conditions of the physical problem being solved.
Jim Branson 2012-10-21