A Little General Relativity

Special Relativity extends the symmetry of the laws of physics in inertial frames of reference. Newton's laws had this symmetry but were not correct at large velocities and electromagnetism with the speed of light showed us how to extend this principle, by going to 4 dimensions.

Newton's gravity also had the somewhat surprising symmetry, that the force of gravity is proportional to the same mass used in the calculation of acceleration in $F=ma$. We refer to this as the equality of gravitational mass and inertial mass. Why is the force of gravity proportional to the inertial mass, when other forces don't work this way.

General Relativity explains this by saying that there is no difference between gravity and acceleration. This is called the general principle of equivalence. If we are inside an elevator and feel a ``force'' pushing us down against the floor, we can't tell if it is due to gravity, or the elevator accelerating upward.

This explains why the gravitational mass is equal to the inertial mass. Essentially gravity is an acceleration so there is no ``force of gravity''.

Einstein extended the change of geometry started by Minkowski, to change from the flat geometry of Minkowski space to a 4D geometry which can have curvature. Curvature in spacetime geometry has the effect of producing accelerations.

The Einstein Equation relates the curvature in the geometry to the mass and energy density. It is a tensor equation 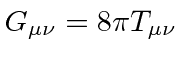$G_{\mu\nu}=8\pi T_{\mu\nu}$, but the math is too complicated for one chapter in this course in mechanics. The study of General Relativity is usually done in a year-long course on this topic alone.

Nevertheless, it is useful to understand the implications of General Relativity and curved spacetime without trying to solve the Einstein equation.