Next: Black Holes Up: Orbits of Photons Previous: Orbits of Photons Contents
With no mass
![]() , the equation reduces to
, the equation reduces to
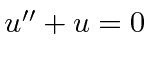 which has the solution
which has the solution
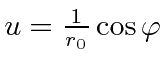 which is the equation of a straight line written in polar coordinates.
Lets
solve the full equation to first order in the small parameter
which is the equation of a straight line written in polar coordinates.
Lets
solve the full equation to first order in the small parameter
![]() .
The full solution will be the solution for with
.
The full solution will be the solution for with
![]() plus a small perturbation due to the mass.
plus a small perturbation due to the mass.
 |
|||
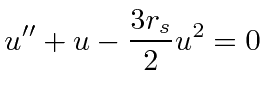 |
the differential equation | ||
 |
plug in aprox. |
||
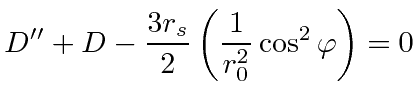 |
drop terms higher order in |
||
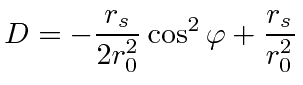 |
guess solution, plug in hw |
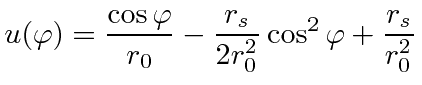 |
We can rather simply
compute the deflection of light from this.
At large
![]() ,
,
![]() and for small
and for small
![]() we
expect
we
expect
![]() to be near to
to be near to
![]() there.
there.
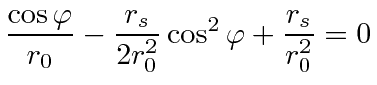 |
|
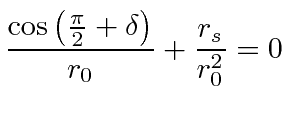 |
|
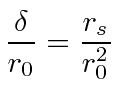 |
|
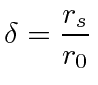 |
 so the total angular deflection of light is
so the total angular deflection of light is
 |
Jim Branson 2012-10-21