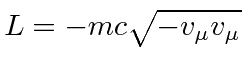The Geodesic Equation

Particles follow a geodesic through the curved spacetime. This is analogous to taking a great circle route on the curved surface of the earth. We minimize $S$ to take the shortest path, the geodesic.

$$S = -mc\int\limits_{\tau_i}^{\tau_f} \sqrt{-ds^2}$$

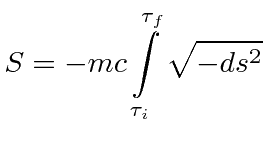
We may take the Action back to an integral over proper time if that is more convenient.

$$S= -mc\int\limits_{\tau_i}^{\tau_f} \sqrt{-ds... ...u}} d\tau = -mc\int\limits_{\tau_i}^{\tau_f} \sqrt{-v_\mu v_\mu} d\tau$$

This is a simple version of the geodesic equation that will be adequate for our purposes. General Relativity will need to deal with the problem of the correct geodesic in a more complex but also more generally correct way.

The Euler-Lagrange equation to minimize this Action is

$${\partial L\over\partial x_\mu}-{d\over d\tau}{\partial L\over\partial \dot{x}_\mu}=0$$

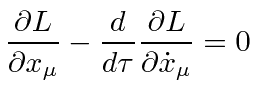
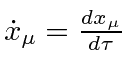where $\dot{x}_\mu={d x_\mu\over d\tau}$ and

$$L=-mc\sqrt{-v_\mu v_\mu}$$