Next: The Schwarzschild Metric Up: A Little General Relativity Previous: Geometries Contents
In the Riemannian geometry of General Relativity,
lengths (dot products) are computed using a metric tensor
which depends on the stress-energy tensor
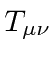 in Einstein's equation.
In flat Minkowski space:
in Einstein's equation.
In flat Minkowski space:
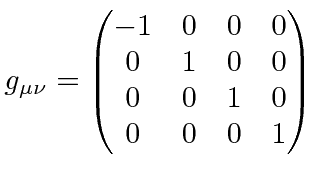
 .
.
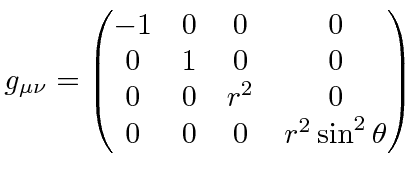
The usual way to keep track of dot products etc. is to introduce upper and lower indices on vectors (and tensors). A dot product is defined to be between one vector with a lower index and another with an upper index.
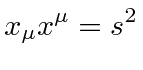
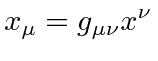
The simplest example is the solution of the Einstein equations by Schwarzschild for problems with spherical symmetry.
Jim Branson 2012-10-21