The Schwarzschild Metric

Schwarzschild solved the Einstein equations under the assumption of spherical symmetry in 1915, two years after their publication. This in itself is a good indication that the equations of General Relativity are a good deal more complicated than Electromagnetism.

The most obvious spherically symmetric problem is that of a point mass. The mass curves space-time and thus affects the particles moving nearby. The metric tensor in Schwarzschild (spherical coordinates becomes

$$g_{\mu\nu}=\begin{pmatrix}-\left(1 - \frac{r_... ...r_s}{r} \right)} &0&0\cr 0&0&r^2&0\cr0&0&0&r^2\sin^2\theta\end{pmatrix}$$

and the space-time interval in spherical coordinates in the Schwarzschild solution is.

$${ds}^{2} =-c^2{d\tau}^2 = -\left(1 - \frac{r... ...\frac{r_s}{r}} + r^2 \left(d\theta^2 + \sin^2\theta \, d\varphi^2\right)$$

where $\tau$ is the proper time (time measured by a clock moving with the particle) in seconds, $t$ is the coordinate time (measured by a stationary clock at infinity) in seconds, $r$ is the radial coordinate (circumference of a circle centered on the star divided by $2\pi$) in meters, $\theta$ is the polar angle, $\varphi$ is the azimuthal angle, and $r_s$ is the Schwarzschild radius (in meters) of the massive body, which is related to its mass $M$ by.

$$r_{s} = \frac{2GM}{c^{2}}$$

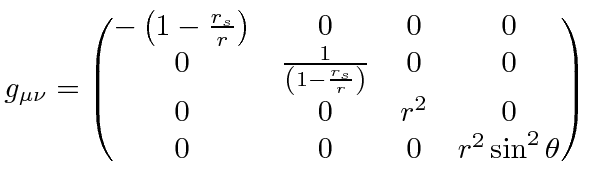
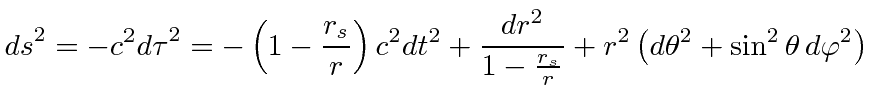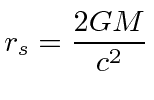This goes to the normal flat Minkowski space-time interval (in spherical coordinates) for $r\rightarrow\infty$ or for zero mass $M$.

The Schwarzschild radius for normal planets and stars is much smaller than the actual size of the object so the Schwarzschild solution is only valid outside the object. For black holes, the Schwarzschild radius is the horizon inside of which nothing can escape the black hole.