Next: The Singularity in Schwarzschild Up: A Little General Relativity Previous: The Schwarzschild Metric Contents
We may
consider how the proper time for a particle
![]() relates to the coordinate time
relates to the coordinate time
![]() as a function of distance from
the mass at the origin.
In the rest frame of the particle,
as a function of distance from
the mass at the origin.
In the rest frame of the particle,
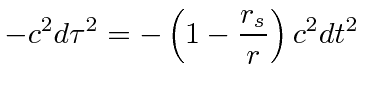
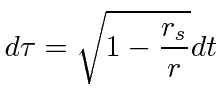
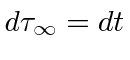
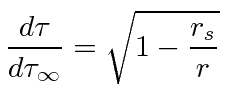 |
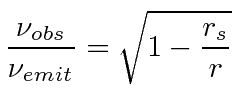
Since the energy of a photon is
![]() , the
photon loses energy as it moves outward in the gravitational field.
, the
photon loses energy as it moves outward in the gravitational field.
Jim Branson 2012-10-21