Next: Orbits of Photons Up: A Little General Relativity Previous: Conserved Energy and Angular Contents
Start with the
dot product of the 4-momentum with itself and use the conserved quantities above to
eliminate
![]() and
and
![]() .
.
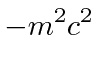 |
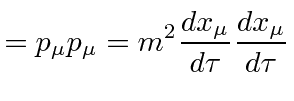 |
|
![$\displaystyle = -m^2 \left[\left(1 - \frac{r_s}{r} \right) c^2 \dot{t}^2 - \frac{\dot{r}^2}{1-\frac{r_s}{r}} - r^2 \dot{\varphi}^2\right]$](img1145.png) |
||
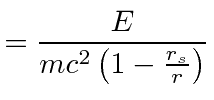 |
||
 |
||
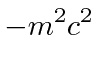 |
![$\displaystyle = -m^2 \left[\left(1 - \frac{r_s}{r} \right) {E^2\over m^2c^2\lef...
...r} \right)^2} - \frac{\dot{r}^2}{1-\frac{r_s}{r}} - {L_z^2\over m^2r^2} \right]$](img1150.png) |
|
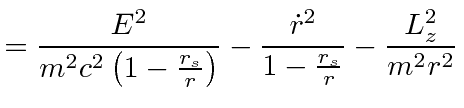 |
||
 |
||
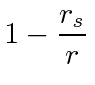 |
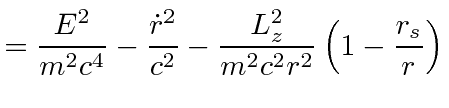 |
|
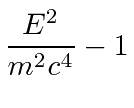 |
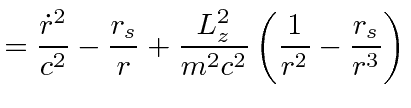 |
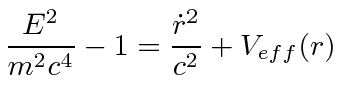 |
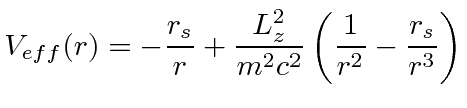 |
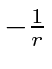 gravitational potential and the normal
gravitational potential and the normal
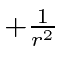 angular momentum pseudopotential.
There is an additional term proportional to
angular momentum pseudopotential.
There is an additional term proportional to
The
effective potential will increase sharply as we go out from
![]() ,
then potentially
reach a maximum, drop to a minimum, then increase as
,
then potentially
reach a maximum, drop to a minimum, then increase as
![]() .
It is around the minimum that there can be a stable bound orbit.
As in Newtonian gravity, the particle may have sufficient energy to escape to infinity.
In the Schwarzschild solution, it may also have enough energy to go over the angular momentum barrier and fall down to the
Schwarzschild radius.
As seen from infinity, it takes an infinite amount of time to reach
.
It is around the minimum that there can be a stable bound orbit.
As in Newtonian gravity, the particle may have sufficient energy to escape to infinity.
In the Schwarzschild solution, it may also have enough energy to go over the angular momentum barrier and fall down to the
Schwarzschild radius.
As seen from infinity, it takes an infinite amount of time to reach
![]() , but from the frame of the particle,
it can quickly go to
, but from the frame of the particle,
it can quickly go to
![]() .
.
We can find the positions of the maximum and minimum effective potential and the conditions under which there will be a minimum.
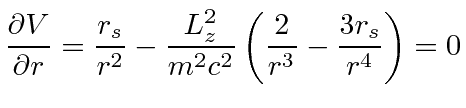 |
|
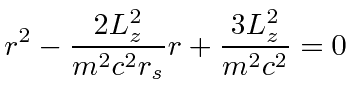 |
|
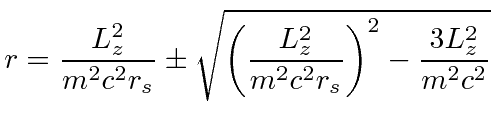 |
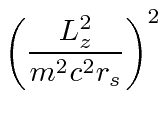 |
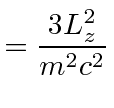 |
different powers of |
|
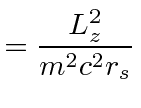 |
|||
 |
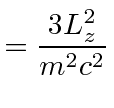 |
use |
|
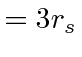 |
radius below which there are no solutions |
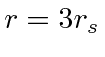 , independent of
, independent of
Jim Branson 2012-10-21