For the purposes of brevity and clarity, let us define the inertial frame
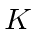 to be at rest in the lab with coordinates
to be at rest in the lab with coordinates
 and define another inertial frame
and define another inertial frame
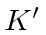 to coincide with
to coincide with
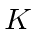 at
at
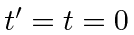 and to be moving relative to
and to be moving relative to
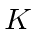 with a velocity
with a velocity
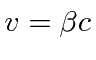 in the x direction.
in the x direction.
- Assume an object of length
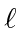 is at rest in the
is at rest in the 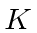 frame.
Show that the expression for the Lorentz contraction can be obtained if an observer in the
frame.
Show that the expression for the Lorentz contraction can be obtained if an observer in the 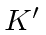 frame measures the time it takes
for an object to pass and multiplies by the velocity
frame measures the time it takes
for an object to pass and multiplies by the velocity 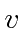 .
.
- Two events take place at the same time but at positions differing by
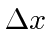 in the
in the 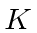 frame.
Calculate the difference in position
frame.
Calculate the difference in position 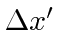 and the difference in time
and the difference in time 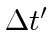 in the
in the 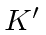 frame.
frame.
- Clocks located at the origins of the
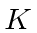 and
and 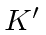 frames are synchronized at
frames are synchronized at 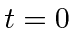 .
At a time
.
At a time  , an observer at the origin of the
, an observer at the origin of the 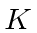 system uses a telescope to read the the clock moving with the
system uses a telescope to read the the clock moving with the 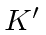 system.
What time does he read.
system.
What time does he read.
- A relativistic rocket emits exhaust gasses with a constant velocity
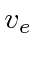 in the rest frame of the rocket
and at a rate
in the rest frame of the rocket
and at a rate
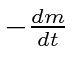 .
Show that the equation of motion for the rocket is
.
Show that the equation of motion for the rocket is
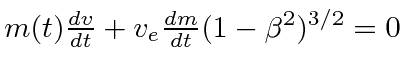 ,
where
,
where 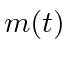 is the mass of the rocket.
is the mass of the rocket.
- A muon is an unstable particle with a mean lifetime of 2 microseconds in its rest frame and a mass
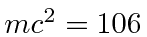 MeV.
What is its mean lifetime in the frame of the earth if its energy is
MeV.
What is its mean lifetime in the frame of the earth if its energy is 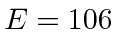 GeV.
GeV.
- A nearby star is found to be moving away from the earth with a velocity of
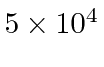 m/s by measuring the
Balmer
m/s by measuring the
Balmer 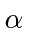 (H-alpha) wavelength normally
(H-alpha) wavelength normally
 nm.
How much and in what directions is the wavelength shifted?
nm.
How much and in what directions is the wavelength shifted?
- An astronaut travels to a nearby star system, a distance of 11 light years away, and returns.
Both legs of the trip are made at a velocity of
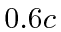 .
How much have the astronaut and his twin on earth aged?
.
How much have the astronaut and his twin on earth aged?
- The total solar radiation at the position of the earth (
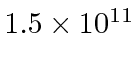 m from the sun) is measured by satellite to be 1,366 W/m
m from the sun) is measured by satellite to be 1,366 W/m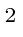 .
How much mass per second is converted to energy in the sun?
.
How much mass per second is converted to energy in the sun?
- What is the kinetic energy of a particle of mass
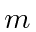 and momentum
and momentum 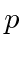 ?
?
- LEP collided electrons with positrons with a center of mass energy of 208 GeV.
The two particles have the same energy (104 GeV) in the lab.
What is
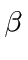 for these particles?
for these particles?
- A neutral pion (
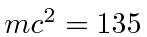 MeV) has a energy of 40 GeV.
It decays into two photons.
If the two photons have the same energy in the lab frame, what is the angle between them?
MeV) has a energy of 40 GeV.
It decays into two photons.
If the two photons have the same energy in the lab frame, what is the angle between them?
- A neutron (
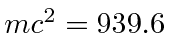 MeV) decays into a proton (
MeV) decays into a proton (
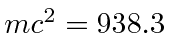 MeV) and an electron (
MeV) and an electron (
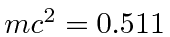 MeV) and
an antineutrino (
MeV) and
an antineutrino (
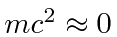 MeV).
The decay is symmetric so that the three final state particles lie in a plane separated by angles of 120 degrees.
What is the momentum of each particle?
What is the kinetic energy of each particle?
What trend do you notice?
MeV).
The decay is symmetric so that the three final state particles lie in a plane separated by angles of 120 degrees.
What is the momentum of each particle?
What is the kinetic energy of each particle?
What trend do you notice?
- Use the Lorentz transformation to derive the velocity addition formula.
- A spacecraft passes Neptune with a speed of
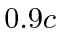 relative to the planet.
A second spacecraft, more urgently exploring the outer solar system,
is observed to pass the first one (in exactly the same direction) at a speed of
relative to the planet.
A second spacecraft, more urgently exploring the outer solar system,
is observed to pass the first one (in exactly the same direction) at a speed of 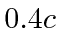 .
What is the speed of the second spacecraft relative to Neptune?
.
What is the speed of the second spacecraft relative to Neptune?
- Show that the relativisticly corrected form of Newton's Second Law is.
- Calculate the kinetic energy of a particle scattered through an angle
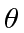 by a target particle of equal mass.
Assume the target particle is at rest and that the incident particle has kinetic energy
by a target particle of equal mass.
Assume the target particle is at rest and that the incident particle has kinetic energy 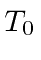 .
.
- Calculate the dot product of the velocity 4-vectors for two particles,
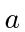 and
and 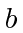 .
Show how it depends on the relative velocity of the two particles.
.
Show how it depends on the relative velocity of the two particles.
- In modern High Energy physics, most particle accelerators collide beams of equal energy particles
rather than collide a beam with a target that is at rest.
Assume we want to collide protons with protons.
Calculate a formula for the ``Center of Mass'' energy of the collisions for the case of a fixed target.
The Large Hadron Collider will have a center of mass energy of 14,000 GeV.
What energy beam would be needed to achieve this center of mass energy by colliding with a fixed
target of protons (Liquid Hydrogen)?
- Assume a neutrino beam is made by generating a beam of
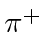 with kinetic energy
with kinetic energy 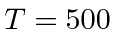 GeV.
The
GeV.
The 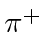 decay to a positive muon and a neutrino of the muon type,
decay to a positive muon and a neutrino of the muon type,
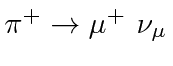 .
What is the energy range of neutrinos in the beam if we define the ``beam'' to be in the direction of
the original pion beam within and small angle of
.
What is the energy range of neutrinos in the beam if we define the ``beam'' to be in the direction of
the original pion beam within and small angle of
 radians?
radians?
- Show that Maxwell's equations written in 3D and in Rationalized Heavyside-Lorentz Units, can all be derived from
the 4D Maxwell's equation in conjunction with the definition of
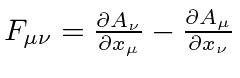 .
.
- Assume the relativistic motion of a particle in 4D is simply given by
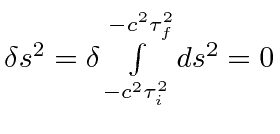 .
Show that this leads to the standard non-relativistic Lagrange equation for a particle with no forces
acting on it.
.
Show that this leads to the standard non-relativistic Lagrange equation for a particle with no forces
acting on it.
Jim Branson
2012-10-21
![]() to be at rest in the lab with coordinates
to be at rest in the lab with coordinates
![]() and define another inertial frame
and define another inertial frame
![]() to coincide with
to coincide with
![]() at
at
![]() and to be moving relative to
and to be moving relative to
![]() with a velocity
with a velocity
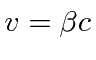 in the x direction.
in the x direction.
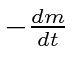 .
Show that the equation of motion for the rocket is
.
Show that the equation of motion for the rocket is
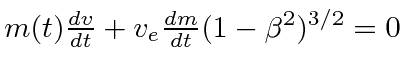 ,
where
,
where 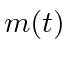 is the mass of the rocket.
is the mass of the rocket.
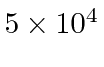 m/s by measuring the
Balmer
m/s by measuring the
Balmer 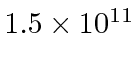 m from the sun) is measured by satellite to be 1,366 W/m
m from the sun) is measured by satellite to be 1,366 W/m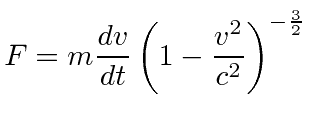
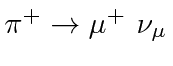 .
What is the energy range of neutrinos in the beam if we define the ``beam'' to be in the direction of
the original pion beam within and small angle of
.
What is the energy range of neutrinos in the beam if we define the ``beam'' to be in the direction of
the original pion beam within and small angle of
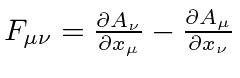 .
.
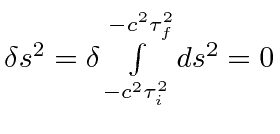 .
Show that this leads to the standard non-relativistic Lagrange equation for a particle with no forces
acting on it.
.
Show that this leads to the standard non-relativistic Lagrange equation for a particle with no forces
acting on it.