Vectors and Rotations

The laws of Physics are ``invariant'' under rotations of the coordinate system.

Rotational symmetry of laws of Physics implies conservation of Angular Momentum.

We will work with ``Passive Rotations'' where we rotate the coordinate axes rather than ``active rotations'' where we rotate the physical system and keep the axes fixed. These are essentially the same thing except the rotation angle changes sign.

A vector is a mathematical object that transforms in a particular way under rotations.

We know there are also physical quantities called scalars that are invariant under rotations.

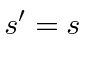
$\displaystyle s'=s$

An example is the mass of an object or a particle, $\bgroup\color{black}$ m'=m$\egroup$ .

Assume (for now) that we live in three dimensions. The position in three-space is an important example of a vector.

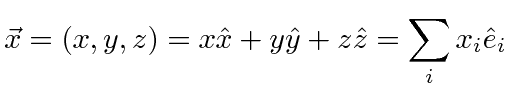
$\bgroup\color{black}$\displaystyle \vec{x}=(x,y,z)=x\hat{x}+y\hat{y}+z\hat{z}=\sum\limits_i x_i \hat{e}_i $\egroup$

The $\bgroup\color{black}$ \hat{e}_i$\egroup$ are three orthogonal unit vectors.

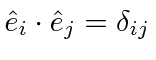$\bgroup\color{black}$ \displaystyle \hat{e}_i\cdot\hat{e}_j=\delta_{ij} $\egroup$

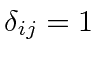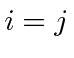This the Kronecker delta, $\bgroup\color{black}$ \delta_{ij}=1$\egroup$ for $\bgroup\color{black}$ i=j$\egroup$ and zero otherwise.

The dot product of two vectors is a scalar, and therefore invariant under rotations of the coordinate system.

$\bgroup\color{black}$\displaystyle \vec{v}\cdot\vec{x}=v_x x+ v_y y +v_z z=v_1 x_1 + v_2 x_2 +v_3 x_3 = \sum\limits v_i x_i $\egroup$

This makes sense physically since the length of a vector should not depend on a rotation of the coordinates.

We will often use the Einstein summation convention: repeated indices imply a sum over that index.

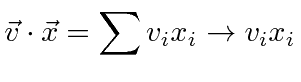
$\bgroup\color{black}$\displaystyle \vec{v}\cdot\vec{x}= \sum\limits v_i x_i \rightarrow v_i x_i $\egroup$

The repeated index is a dummy index.

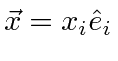
$\bgroup\color{black}$\displaystyle \vec{x}=x_i \hat{e}_i $\egroup$

$\bgroup\color{black}$ \displaystyle \vec{v}\cdot\vec{x}= v_i x_i $\egroup$

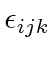We will also use the totally antisymmetric tensor $\bgroup\color{black}$ \epsilon_{ijk}$\egroup$ . It changes sign if any of the three indices are interchanged. Its value is one for any cyclic permutation of the indices and minus one for an anticyclic permutation. It must be zero if any index is repeated since it is antisymmetric.

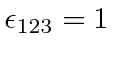	$\displaystyle \epsilon_{123}=1$
	$\displaystyle \epsilon_{132}=-1$
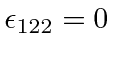	$\displaystyle \epsilon_{122}=0$
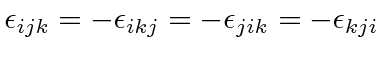	$\displaystyle \epsilon_{ijk}=-\epsilon_{ikj}=-\epsilon_{jik}=-\epsilon_{kji}$
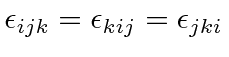	$\displaystyle \epsilon_{ijk}=\epsilon_{kij}=\epsilon_{jki}$

We use this antisymmetric tensor to write a cross product between two vectors.

$\bgroup\color{black}$\displaystyle \vec{v}\times\vec{x}=v_ix_j\epsilon_{ijk}\hat{e}_k $\egroup$

The expression for the $\bgroup\color{black}$ k$\egroup$ component of the cross product is simpler.

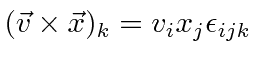$\bgroup\color{black}$ \displaystyle (\vec{v}\times\vec{x})_k=v_ix_j\epsilon_{ijk} $\egroup$

Here the sum over $\bgroup\color{black}$ i$\egroup$ and $\bgroup\color{black}$ j$\egroup$ are implied by the Einstein convention, so we can do the example of the $\bgroup\color{black}$ z$\egroup$ component of the cross product omitting all the terms in the sum for which an index is repeated and $\bgroup\color{black}$ \epsilon$\egroup$ is zero.

$\bgroup\color{black}$\displaystyle (\vec{v}\times\vec{x})_3 =v_ix_j\epsilon_{ij3}=v_1x_2-v_2x_1=v_x y-v_y x $\egroup$

Subsections

Jim Branson 2012-10-21