Next: The Vector Derivative Up: Vectors and Rotations Previous: Cross Products and Axial Contents
For our passive rotations, we will change from one orthonormal, right-handed basis to another orthonormal,
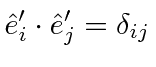
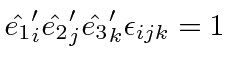
If we rotate the coordinate axes, we can compute a vector in the new (primed) coordinates from the original vector by multiplying by a Rotation Matrix.
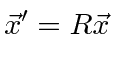
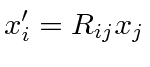 |
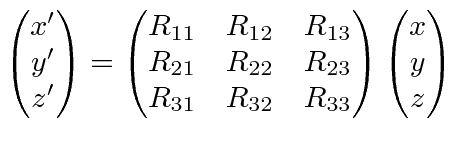
With a little thought, we can
compute the elements of the rotation matrix.
Lets compute the vector
![]() , the position vector in the rotated coordinates.
To get the
, the position vector in the rotated coordinates.
To get the
![]() component of
component of
![]() , just take the vector and dot it into the new unit vector
, just take the vector and dot it into the new unit vector
![]() , written in the original coordinates.
, written in the original coordinates.
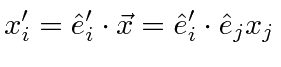
So the rotation matrix is just given by
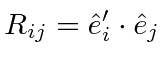 |
Thus, each element of the rotation matrix is simply the cosine of the angle between a new coordinate axis and an old coordinate axis.
It is easy to see physically that the product of two rotations is just some other rotation.
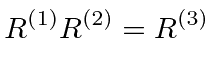
As an example, lets make a rotation through a small angle
![]() in the
in the
![]() plane, leaving the
plane, leaving the
![]() axis unchanged.
The angle between the
axis unchanged.
The angle between the
![]() and the
and the
![]() axis is
axis is
![]() .
The angle between the
.
The angle between the
![]() and the
and the
![]() axis is also
axis is also
![]() .
The angle between the
.
The angle between the
![]() and the
and the
![]() axis is
axis is
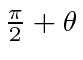 .
The angle between the
.
The angle between the
![]() and the
and the
![]() axis is
axis is
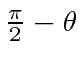 .
The angle between the
.
The angle between the
![]() and the
and the
![]() axis is 0.
All the other angle with the
axis is 0.
All the other angle with the
![]() axis are
axis are
![]() .
.
So we can write the rotation matrix.
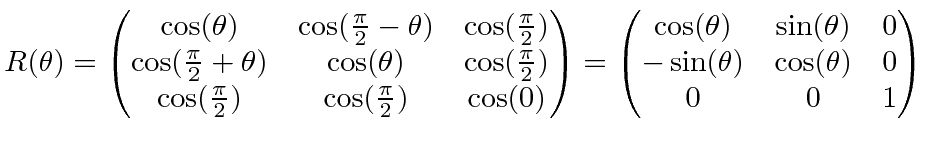
In three dimensions, a rotation in the
![]() plane can be said to be a
rotation about the
plane can be said to be a
rotation about the
![]() axis.
This is not true in four dimensions.
axis.
This is not true in four dimensions.
One can write the dot product between two vectors just in terms of the lengths of vectors.
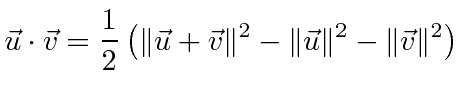
Lets use the fact that dot products are invariant to derive a property of the rotation matrices.
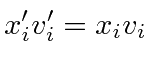 |
||
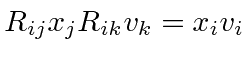 |
||
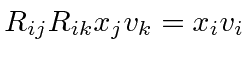 |
||
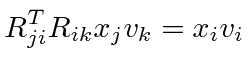 |
||
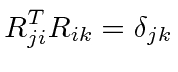 |
||
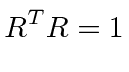 |
||
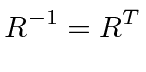 |
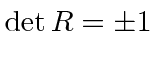 .
.
Any rotation in three dimensions can be written as a rotation in some plane or as a rotation about an axis orthogonal to that plane.
We can describe a constantly rotating coordinate system as a rotation in a plane by and angle
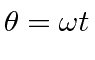
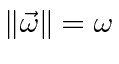 .
The rotation matrix depends on time.
Since
.
The rotation matrix depends on time.
Since
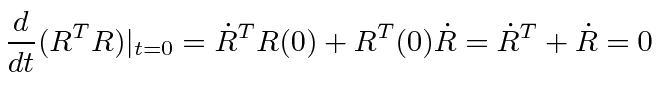
Jim Branson 2012-10-21