Next: Cross Products and Axial Up: Vectors and Rotations Previous: Vectors and Rotations Contents
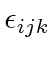 .
.
First, lets do the scalar triple product of vectors. Note that this product is completely symmetric among the three vectors once its written in our notation. Its simply cyclic combinations have a plus sign and anticyclic have a minus sign.
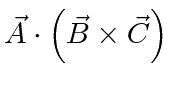 |
 |
|
 |
||
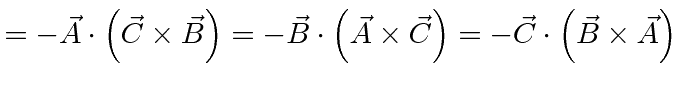 |
The
triple vector product will require us to ``derive'' an identity involving the product of
two
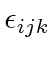 s.
s.

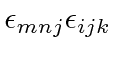 .
Note that the index
.
Note that the index
We now do the sum
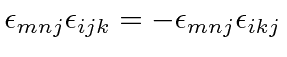 .
First of all
.
First of all
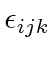 will be zero if any of the indices are repeated.
So me must have
will be zero if any of the indices are repeated.
So me must have
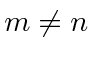 and
and
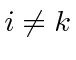 .
We will sum over
.
We will sum over
![]() , but starting from the first
, but starting from the first
![]() ,
,
![]() must be the other index besides the two used up for
must be the other index besides the two used up for
![]() and
and
![]() so there is only one non-zero term in the sum.
This is also true for the second
so there is only one non-zero term in the sum.
This is also true for the second
![]() .
Since the index
.
Since the index
![]() in the two tensors is the same we must have
in the two tensors is the same we must have
![]() and
and
![]() using up the same two indices that
using up the same two indices that
![]() and
and
![]() do.
So the two possibilities are
do.
So the two possibilities are
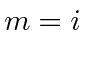 |
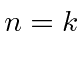 |
||
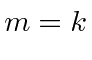 |
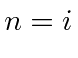 |
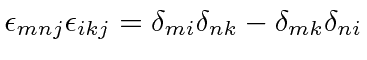 |
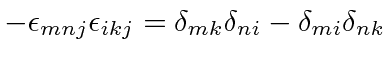
We can now easily compute the triple vector product identities.
![$\displaystyle \left[\vec{A}\times\left(\vec{B}\times\vec{C}\right)\right]_k$](img51.png) |
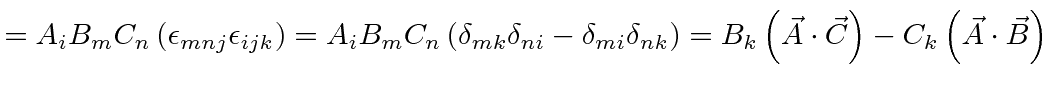 |
|
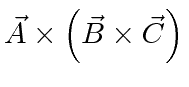 |
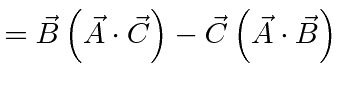 |
For expressions involving derivatives in 3D, these tools become even more useful.
Jim Branson 2012-10-21