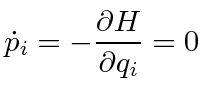Conserved Momenta

If the Hamiltonian is independent of one of the coordinates ( symmetry), then the second Hamilton's equation implies that the conjugate momentum is conserved.

$$\dot{p}_i=-{\partial H\over\partial q_i }=0$$

This usually means very simple (constant velocity) motion in this coordinate, reducing the dimensionality of the problem to be solved.