Next: Example: Particle in 3D Up: Hamiltonian Mechanics Previous: Conserved Momenta Contents
Consider a
particle constrained to move on the surface of a cylinder of radius
![]() , with a force toward the origin
, with a force toward the origin
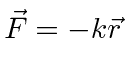 .
We will work the problem in cylindrical coordinates,
.
We will work the problem in cylindrical coordinates,
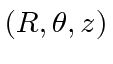 with
with
![]() fixed.
It is rather simple to work this problem from Newton's laws for from the Lagrangian so the point of this exercise is only to see that
the Hamiltonian formalism has a lot in common with the methods we know.
fixed.
It is rather simple to work this problem from Newton's laws for from the Lagrangian so the point of this exercise is only to see that
the Hamiltonian formalism has a lot in common with the methods we know.
Of course the potential energy is
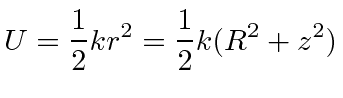

Since the potential does not depend on the velocities,
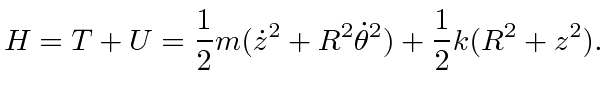
We need to write this as a function of the coordinates and momenta.
So
first find the momenta conjugate to
![]() and
and
![]() .
.
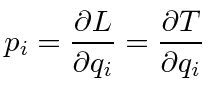
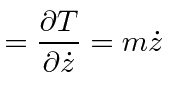 |
||
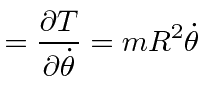 |
Next we write the Hamiltonian in terms of the momenta.
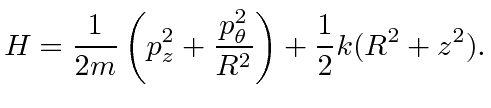
Now we look at
Hamilton's equations.
The equations for
![]() give us the momentum in terms of
give us the momentum in terms of
![]() again and so there is nothing new there.
again and so there is nothing new there.
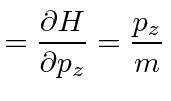 |
||
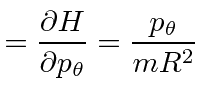 |
The
equations of motion can be found in the equations for
![]()
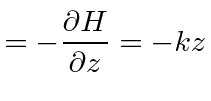 |
||
 |
 |
||
 |
 |
Jim Branson 2012-10-21