The Hamiltonian Formalism

We may define the Hamiltonian in terms of the Lagrangian as in the last section.

$$H(q_i,p_i) = \sum\limits_{i=1}^n p_i \dot{q}_i - L$$

The Hamiltonian is a function of coordinates and conjugate momenta, so the $\dot{q}_i$ must be rewritten in terms of the $p_i$, which is a simple thing to do.

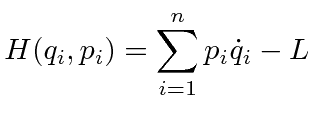
With the Hamiltonian written as a function of the coordinates $q_i$ and the conjugate momenta $p_i$, there are $2n$ first order differential equations of motion, Hamilton's Equations.

$$\dot{q}_i={\partial H\over\partial p_i}$$

$$\dot{p}_i=-{\partial H\over\partial q_i }$$

These equations are fairly simply derived from Lagrange's equations by considering an infinitesimal variation.

$$H(q_i,p_i) = \sum\limits_{i=1}^n p_i \dot{q}_i - L(q_i,\dot{q}_i)$$

$$dH = \sum\limits_k\left({\partial H\over \partial q_k} dq_k + {\part... ...er \partial q_k} dq_k - {\partial L\over \partial \dot{q}_k} d\dot{q}_k \right)$$

$$dH = \sum\limits_k\left({\partial H\over \partial q_k} dq_k + {\part... ...\left(\dot{q}_k dp_k + p_k d\dot{q}_k - \dot{p}_k dq_k - p_k d\dot{q}_k \right)$$

$$dH = \sum\limits_k\left({\partial H\over \partial q_k} dq_k + {\part... ... p_k} dp_k \right) = \sum\limits_k\left(\dot{q}_k dp_k - \dot{p}_k dq_k \right)$$

$$\dot{q}_i ={\partial H\over\partial p_i}$$

$$\dot{p}_i =-{\partial H\over\partial q_i }$$

(I have not bothered with the explicit time dependence of the Hamiltonian or Lagrangian.)

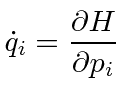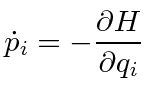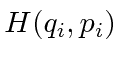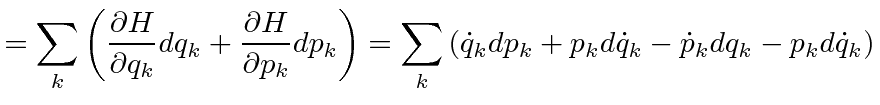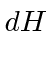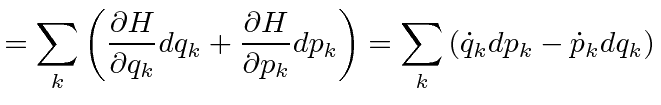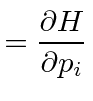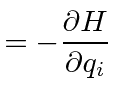Using Hamilton's equations, one quickly identifies conserved momenta and is left with first order differential equations. Usually one of these just gives the momentum and the other is equivalent to the second order Lagrange equation.