Next: The Hamiltonian Formalism Up: Hamiltonian Mechanics Previous: Hamiltonian Mechanics Contents
 |
|
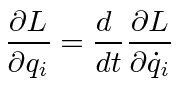 |
We may
define the conjugate momentum to the coordinate
![]() as
as
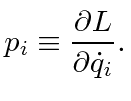

Recall that symmetries or invariances give us some conserved quantities in physics. An important example of this is the time independence of the Lagrangian.
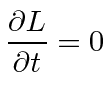
 |
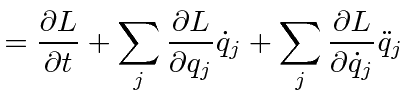 |
chain rule | |
 |
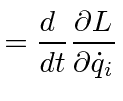 |
Lagrange eq. | |
 |
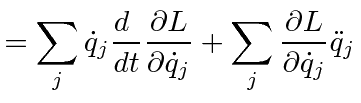 |
plug and 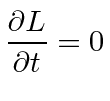 |
|
 |
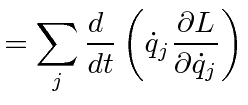 |
||
 |
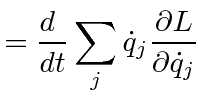 |
sum is total derivative | |
 |
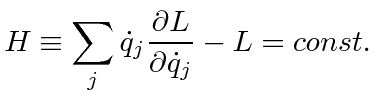
Recall that by Euler's theorem
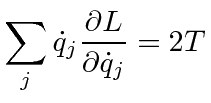
So, if the Potential is velocity independent (remember this) then
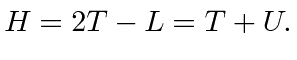
An important exception to this is Electromagnetism where the magnetic force is velocity dependent and hence the Hamiltonian is not simply
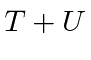 , however, it does represent the total energy including the energy in the EM field.
The Hamiltonian for an electron in an electromagnetic field is.
, however, it does represent the total energy including the energy in the EM field.
The Hamiltonian for an electron in an electromagnetic field is.
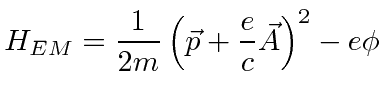
Jim Branson 2012-10-21