Rotating Coordinate System

The arithmetic for rotating coordinate systems can be rather complicated, however, most of the physics can be understood in a relatively simple case. We will first study the simple case, then extend the equations a bit to include the general case.

Since any rotation is just a rotation in a plane, the simple case includes the most general rotation. Our simplification is that we will put two of the coordinate axes in the plane of the rotation. Since we have the choice of coordinate systems in solving our physics problems this covers many cases. But sometimes, like motion on the surface of the earth, we want to define our coordinates in another way and we will deal with that in the next section. In all cases, we will set up our coordinates so that the origin of the inertial coordinate system and the rotating coordinate system coincide.

Imagine we do experiments on a rotating table (rotation in the plane of the table). It is rotating about some point and we will call the point the origin of our coordinate systems.

We know about the ``effective'' centrifugal force $\vec{F}={mv^2\over r}\hat{r}$ from Freshman Physics. If the table is rotating with constant angular frequency $\omega$, we have $v=\omega r$.

$$\vec{F}=m\omega^2r\hat{r}$$

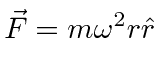
There is another ``effective'' force that depends on velocity called the Coriolis Force. Lets understand this simply by assuming our rotating table is a frictionless air table. For our first experiment we will send a puck straight across the table through the origin. The puck goes from radius $r=r_1$ to radius $r=0$ and back to radius $r_1$ in our experiment and we give the puck exactly the right velocity so that it makes this trip while the table undergoes exactly one half turn.

$$v={2r_1\over \pi/\omega}={2\omega r_1\over\pi}$$

So far, we are talking about the motion observed from a non-rotating frame with the same origin. The puck moves in a straight line at constant velocity from one side of the table to the other as shown in the figure below.

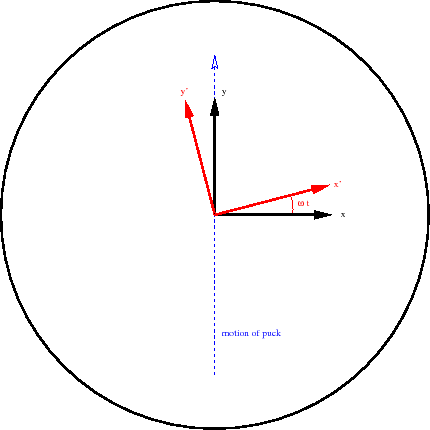
Now lets see what happens using the rotating coordinate system. The figure below gives a rough drawing of the puck's path in the rotating coordinate system. It does not move in a straight line.

The puck starts out with an inward radial velocity as before but also has a large tangential component. The tangential component decreases as the puck gets close to the origin. It goes through the origin then returns to radius $r_1$ on a path symmetric with the one into the origin. (It comes back to the same point because of the velocity we have chosen for this experiment.)

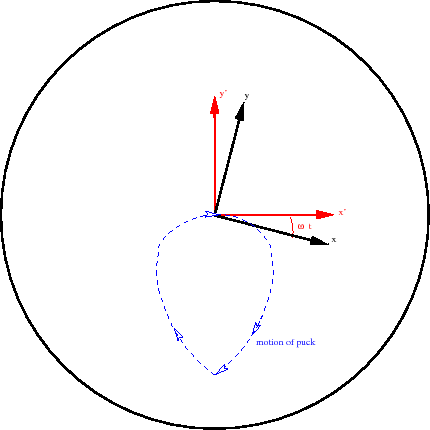
In the rotating frame, there was clearly some effective force that was not radially outward. That was the Coriolis force.