Next: Calculating the Effective Force Up: Rotating Coordinate System Previous: Rotating Coordinate System Contents
To calculate the
effective force in a simple way we will use the rotating table coordinate systems
and calculate the force at
![]() when the two coordinate systems are aligned.
The forces due to the rotation do not depend on time so this is still general.
It will be best to work with the
transformation from the rotating (primed) frame to the inertial frame.
when the two coordinate systems are aligned.
The forces due to the rotation do not depend on time so this is still general.
It will be best to work with the
transformation from the rotating (primed) frame to the inertial frame.
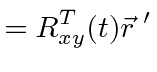 |
||
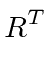 |
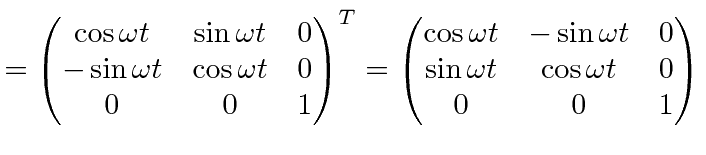 |
|
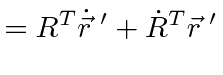 |
||
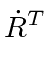 |
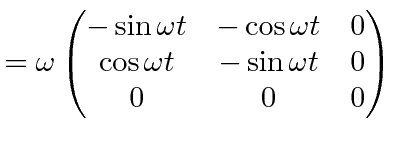 |
|
 |
||
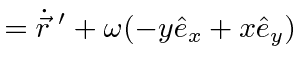 |
||
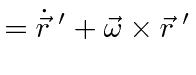 |
This last equation is an important one.
It actually holds for the time derivative of any vector, not just
![]() .
So far it is only true when the coordinate axes coincide like at
.
So far it is only true when the coordinate axes coincide like at
![]() but,
since it is true for any vector, we can apply it to
but,
since it is true for any vector, we can apply it to
![]() .
.
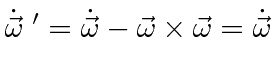
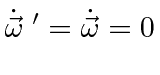
 |
To get the acceleration (and forces), take the second time derivative.
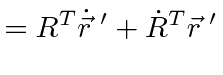 |
||
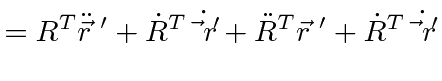 |
||
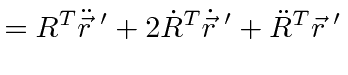 |
||
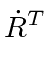 |
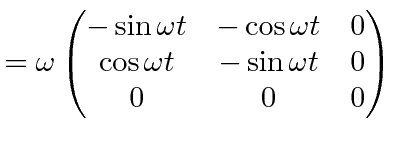 |
|
 |
 |
|
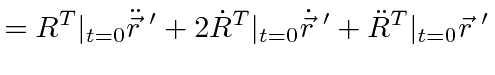 |
||
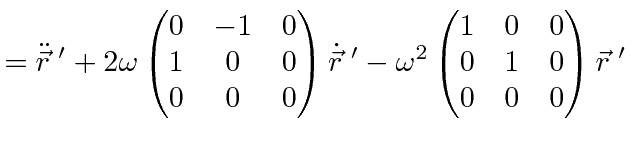 |
||
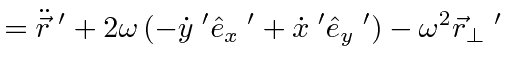 |
||
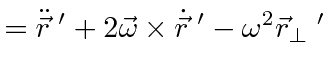 |
||
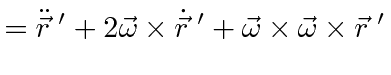 |
||
 |
||
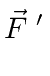 |
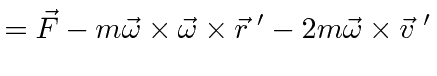 |
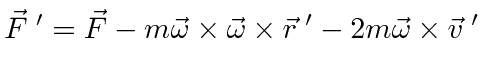 |
Now lets go
back to the first experiment.
First we can compute the
velocity in the rotating frame at
![]() .
(The coordinate axes correspond at
.
(The coordinate axes correspond at
![]() .)
.)
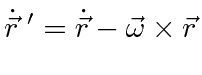 |
||
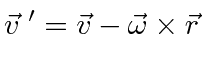 |
||
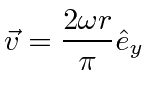 |
||
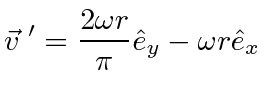 |
Now we can compute the effective force in the rotating frame.
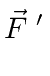 |
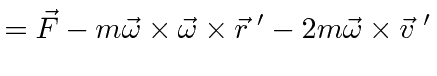 |
|
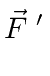 |
 |
|
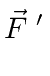 |
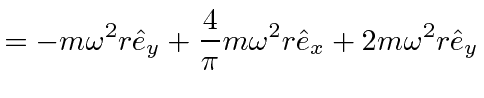 |
|
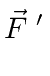 |
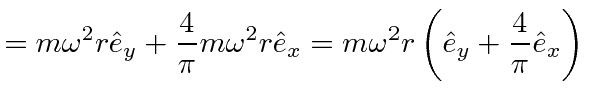 |
This problem is illustrative but not really the usual type of problem where we know the position and velocity in the rotating frame and need to get the effective forces.
Note that a ball flying above the table would have the same behavior since it is only the radius perpendicular to
![]() that acts in the fictitious forces.
that acts in the fictitious forces.
A
second simple experiment would be to place the puck at radius
![]() on the frictionless rotating table,
with no velocity in the inertial frame.
The puck would then just remain motionless in the inertial frame and therefore trace out a circle in the rotating frame.
Lets check this against our equations.
on the frictionless rotating table,
with no velocity in the inertial frame.
The puck would then just remain motionless in the inertial frame and therefore trace out a circle in the rotating frame.
Lets check this against our equations.
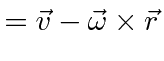 |
||
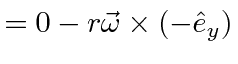 |
||
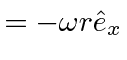 |
||
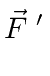 |
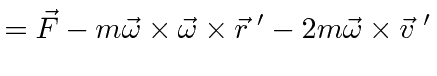 |
|
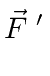 |
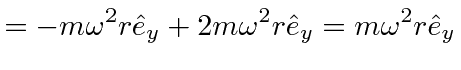 |
Jim Branson 2012-10-21