Next: Compton Scattering Up: Kinematics Problems in Electron Previous: Decay Contents
Nuclei are made up of protons and neutrons. While neutrons are stable inside many nuclei, free neutrons decay with a lifetime of about 15 minutes. This makes them a radiation problem around nuclear reactors, since they can leak out of the reactor and decay. The neutron decays into a proton, an electron, and an antineutrino of the electron type.
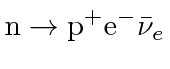
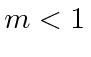 eV.)
eV.)
This is a more complicated problem. Lets count variables. The three final state particles give us 9 variables with only 4 equations to solve. It is usual not to worry about the orientation of the whole decay (unless the initial state is polarized). The three final state particles will lie in a plane (for neutron decay in its rest frame). It takes two variables to define the orientation of the normal to the plane and the event can still be rotated inside the plane so like a rigid body, three angles are needed to describe the overall orientation of the event. Since the laws of physics are symmetric under these rotations, these three variables do not matter. So its fine to have 3 unknown variables at the end but here we have 5.
That means we can have some kind of interesting physics in this decay (that we won't understand here). That is, the final state is not completely given by kinematics. There are two variables undetermined that depend on the physics of the decay.
To make a problem we can solve, we ask the question ``what is the maximum electron energy possible?'' in this decay. The maximum possible energy will occur when both the proton and neutrino recoil directly opposite the electron's direction. If we pick the direction of the electron (2 variables), we have a one dimensional problem with three unknown momenta and just two equations, energy conservation and momentum conservation. We will still need to maximize the electron momentum to get the answer.
Lets work with the three independent variables
![]() ,
,
![]() , and
, and
![]() .
The three energies are.
.
The three energies are.
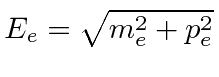 |
||
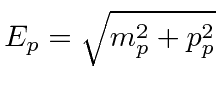 |
||
 |
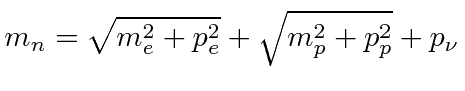 |
||
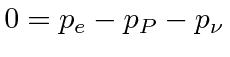 |
||
 |
||
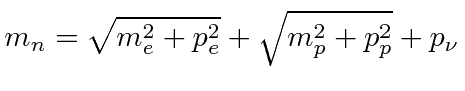 |
||
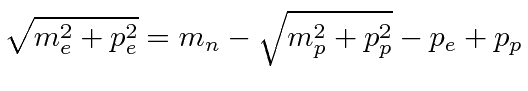 |
||
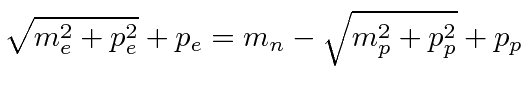 |
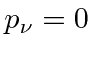 .
Then we have
.
Then we have
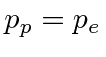 .
.
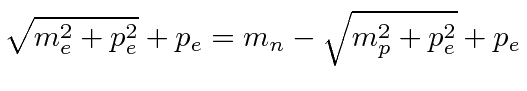 |
||
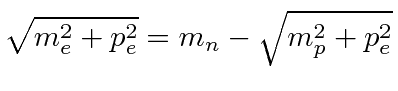 |
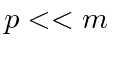 ), so we may approximate its energy by.
), so we may approximate its energy by.
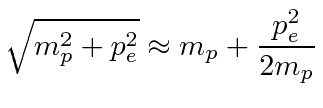 |
||
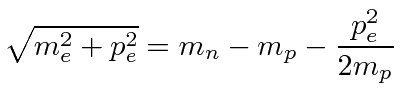 |
||
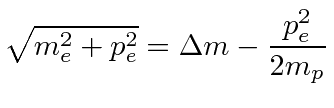 |
||
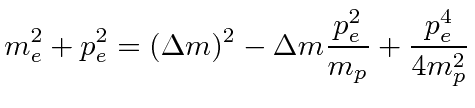 |
||
 |
||
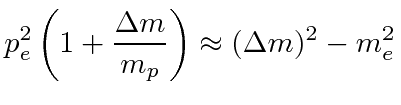 |
||
 |
||
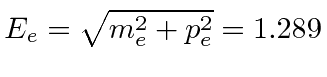 |
When the neutrino momentum is zero, the electron takes nearly all the energy available. The proton, recoiling against it, takes very little energy since it is highly nonrelativistic even though it has the same momentum as the electron.
Jim Branson 2012-10-21