Next: Neutron Decay Up: Kinematics Problems in Electron Previous: Kinematics Problems in Electron Contents
The pions are the lightest (free) particles that interact strongly.
They are substantially lighter than the proton and play an important role in binding nuclei together.
There are three pions, the
![]() , the
, the
![]() , and the
, and the
![]() .
The
.
The
![]() decays rapidly into two photons while the charged pions live for about 20 nanoseconds in its rest frame.
decays rapidly into two photons while the charged pions live for about 20 nanoseconds in its rest frame.
We will analyze the decay of the
![]() into two photons.
The mass of the
into two photons.
The mass of the
![]() is about 135
is about 135
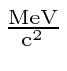 and the photon mass is zero.
and the photon mass is zero.
In all kinematic problems,
the conservation of momentum and energy is best understood as conservation of the 4-momentum.
In the rest frame of the
![]() , the 4-momentum is
, the 4-momentum is
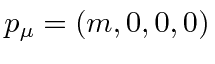 dropping the
dropping the
![]() s from the equation.
The final 4-momentum for photon-1 is
s from the equation.
The final 4-momentum for photon-1 is
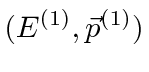 and the final 4-momentum for photon-2 is
and the final 4-momentum for photon-2 is
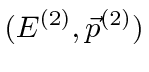 .
4-momentum conservation gives us the 4-vector equation.
.
4-momentum conservation gives us the 4-vector equation.
 |
||
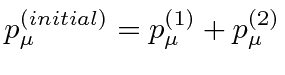 |
||
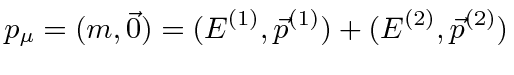 |
||
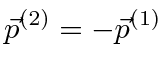 |
||
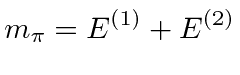 |
||
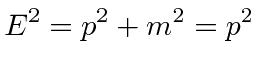 |
||
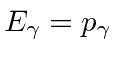 |
||
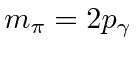 |
The decay goes into two back to back photons each with energy
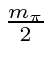 .
If we want to see the result in another frame, we just boost the 4-vector.
.
If we want to see the result in another frame, we just boost the 4-vector.
This is a simple example of using the conservation of 4-momentum to solve a kinematics problem.
We can analyze our solution a little to learn to count the number of variables in a problem.
The initial state is given and 4-momentum is conserved giving us
4 equations.
The
final state has two particles.
If we know the masses, we get
3 unknown variables per final state particle.
That is, an unknown 4-momentum with the requirement that its norm is
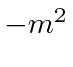 .
.
In
![]() decay, that means we have
4 equations in 6 unknowns and two variables will be left undetermined.
In our solution, these two variables are
the polar and azimuthal angle of one final state photon.
The other photon will go in exactly the opposite direction according to our solution.
decay, that means we have
4 equations in 6 unknowns and two variables will be left undetermined.
In our solution, these two variables are
the polar and azimuthal angle of one final state photon.
The other photon will go in exactly the opposite direction according to our solution.
Jim Branson 2012-10-21