The Twin Paradox

In Special Relativity, it is not possible to transform something from the future into the past or vice versa but we do have the possibility of slowing down aging by using time dilation. To illustrate this we consider a pair of twins, one of whom makes a trip to a nearby star system and returns. This twin will be much younger than the other twin who remained on the earth. This is known as the twin paradox since there is relative motion but it is not obvious which twin should be younger if the laws of physics are independent of inertial frame.

Assume the astronaut twin goes a distance of 8 light years to a star at a speed of $0.8c$ then turns around and returns at the same speed. In the frame of the earth, the trip takes 10 years, while for the astronaut, it takes only 6 years.

$$\ell'={\ell\over\gamma}=0.6\ell$$

The twin on earth ages 20 years while the astronaut ages only 12 years for the round trip. But the relative velocities are symmetric. What does it matter that one makes the trip and one stays on earth?

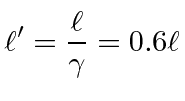
The difference, if there is one, must be in the acceleration at the beginning, middle, or end of the trip. We can analyze the problem using the Doppler shift. Assume the twins synchronize clocks at the beginning of the trip and that they watch each other's clocks (using a telescope) as the trip progresses. The clock frequencies can be computed using the parallel Doppler shift. For simplicity, we assume the clocks tick once per year in their rest frame.

On the outbound trip the twins each observe a clock frequency (of the other's clock)

$$\nu'=\sqrt{1-\beta\over 1+\beta}\ \nu=\sqrt{1-0.8\over 1+0.8}={1\over 3}$$

that is, one tick every three years.

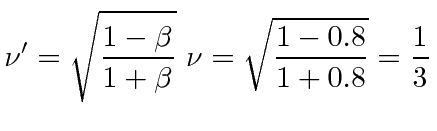
First consider what happens from the earthbound frame. The astronaut twin's clock emits 6 ticks on the trip out. The earthbound twin observes that the trip out takes 18 years receiving one tick every three years. Remember it takes 8 years for the light to get back to earth once the spaceship has reached the star so its reasonable that the observed time is 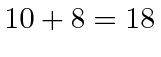$10+8=18$ years. When the ship turns around, the frequency becomes $\nu'=3\nu$. The astronaut's clock emits 6 ticks and the earth twin sees these over 2 years. Thus he sees 12 ticks over 20 years.

From the space ship, The astronaut sees 2 earth clock ticks on the (6 year) trip out and sees 18 ticks on the trip back. So the Doppler shift is completely consistent with the astronaut aging 12 years while the earthbound twin ages 20 years. The difference must be in the acceleration, which we have (over) simplified in this problem.