Next: The Twin Paradox Up: Special Relativity Previous: The 4D Gradient Operator Contents
The sound of a train's horn shifts in frequency as the train passes by due to the relative motion of the train and the one who hears it. Similarly, the frequency of light shifts due to relative motion of the source and observer, even without relativity. Relativity modifies this Doppler Effect due to time dilation.
Consider a source at rest at the origin with an observer moving in the
![]() direction.
We will consider the possibility that the observer is at some distance in
direction.
We will consider the possibility that the observer is at some distance in
![]() .
The beginning of one wavelength is at
.
The beginning of one wavelength is at
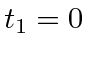 and
and
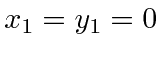 .
The end of the wave is emitted at
.
The end of the wave is emitted at
 and still at
and still at
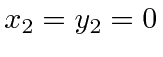 .
This transforms to the observers frame to be at
.
This transforms to the observers frame to be at
 |
||
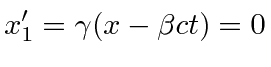 |
||
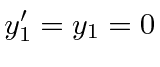 |
||
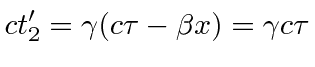 |
||
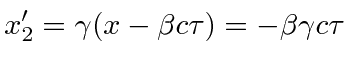 |
||
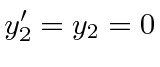 |
||
 |
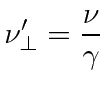
If the observer is moving directly away from the source we have the additional effect of the distance to the observer increasing with time which gives rise to the parallel Doppler effect . The time at which the beginning and end of the wave arrive at the observer is
 |
||
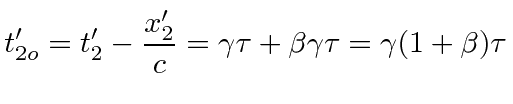 |
||
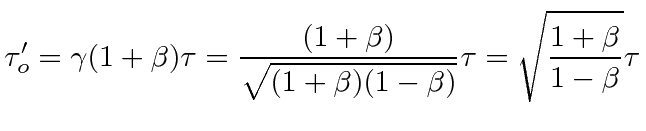 |
||
 |
Jim Branson 2012-10-21