Imaginary Angles

Often physicists use $ict$ as the time component of the 4-vector to make the minus sign in the dot product automatic.

$$x_\mu x_\mu=(ict)^2+x^2+y^2+z^2=-(ct)^2+x^2+y^2+z^2$$

It is interesting to note that if we consider the rapidity as an imaginary angle, then a rotation becomes

$$\mathbb{R}(i\phi)=\begin{pmatrix}\cos(i\phi) & \sin(i\phi) \cr -\... ...ix}\cosh(\phi) & i\sinh(\phi) \cr -i\sinh(\phi) & \cosh(\phi) \cr \end{pmatrix}$$

If we apply this to the vector with $ict$ we get.

$$\begin{pmatrix}x'\cr ict'\end{pmatrix}=\begin{pmatrix}\cosh(\phi)... ...\sinh(\phi) & \cosh(\phi) \cr \end{pmatrix}\begin{pmatrix}x\cr ict\end{pmatrix}$$

$$\begin{pmatrix}x'\cr ict'\end{pmatrix}=\begin{pmatrix}\gamma & i\... ...cr -i\beta\gamma & \gamma \cr \end{pmatrix}\begin{pmatrix}x\cr ict\end{pmatrix}$$

$$\begin{pmatrix}x'\cr ict'\end{pmatrix}=\begin{pmatrix}\gamma x + i\beta\gamma ict \cr -i\beta\gamma x+ \gamma ict \cr \end{pmatrix}$$

$$\begin{pmatrix}x'\cr ict'\end{pmatrix}=\begin{pmatrix}\gamma x -\beta\gamma ct \cr -i\beta\gamma x+ i\gamma ct \cr \end{pmatrix}$$

$$\begin{pmatrix}x'\cr ict'\end{pmatrix}=\begin{pmatrix}\gamma x -\beta\gamma ct \cr i(\gamma ct-\beta\gamma x) \cr \end{pmatrix}$$

$$\begin{pmatrix}x'\cr ct'\end{pmatrix}=\begin{pmatrix}\gamma x -\beta\gamma ct \cr \gamma ct-\beta\gamma x \cr \end{pmatrix}$$

$$\begin{pmatrix}x'\cr ct'\end{pmatrix}=\begin{pmatrix}\gamma & -\b... ... \cr -\beta\gamma & \gamma \cr \end{pmatrix}\begin{pmatrix}x\cr ct\end{pmatrix}$$

This is the same as our Lorentz transformation. It is interesting to note that the transformation, written this way, is an antisymmetric matrix, like the rotation, while it is symmetric when written in terms of the real variable $ct$.

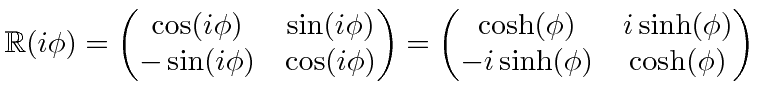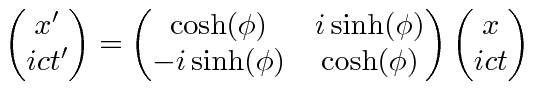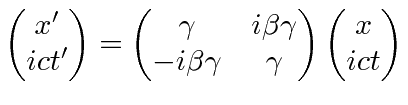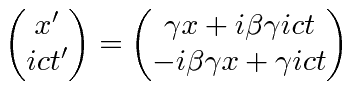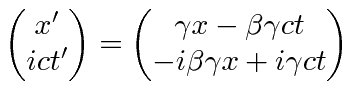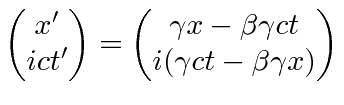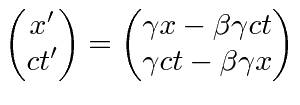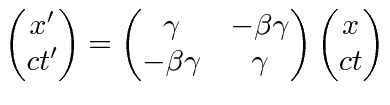The use of $ict$ is quite convenient for calculations on Special Relativity but is frowned upon because General Relativity requires further extensions of geometry for which the fully real version is preferred.