``Rotations'' in 4 Dimensions

Clearly the symmetry transformation in the $xt$ ( a boost) is not identical to that in the $xy$ plane ( a rotation)

$$\mathbb{B}(\beta)=\begin{pmatrix}\gamma & -\beta\gamma\cr -\beta\gamma & \gamma\end{pmatrix}$$

$$\mathbb{R}(\theta)=\begin{pmatrix}\cos(\theta) & \sin(\theta) \cr -\sin(\theta) & \cos(\theta) \cr\end{pmatrix}$$

because there is some difference in the geometry, but they are closely related.

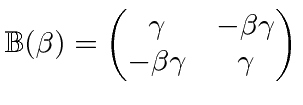Lets try to put in the hyperbolic functions by setting 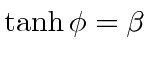$\tanh\phi=\beta$ as the off diagonal terms in the matrix would indicate.

$$\gamma={1\over\sqrt{1-\beta^2}}={1\over\sqrt{... ...hi}-e^{-\phi}\right)^2}} ={{e^{\phi}+e^{-\phi}}\over\sqrt{4}}=\cosh\phi$$

So we see that

$$\beta\gamma=\sinh\phi$$

and the matrix becomes something very similar to the rotation,

$$\tanh\phi=\beta$$

$$\cosh\phi=\gamma$$

$$\sinh\phi=\beta\gamma$$

$$\mathbb{B}(\phi)=\begin{pmatrix}\cosh\phi & -\sinh\phi\cr -\sinh\phi & \cosh\phi\end{pmatrix}$$

$$\phi=\tanh^{-1}\beta$$

where the rapidity $\phi$ plays a role similar to an angle. Like an angle when two subsequent rotations are made in the same plane, the rapidity just adds if two boosts along the same direction are made.

$$\phi=\phi_1+\phi_2$$

This can be easily demonstrated by multiplying the two matrices and using the identities for hyperbolic sine and cosine.

$$\mathbb{B}(\phi_1)\mathbb{B}(\phi_2) =\begin{pmatrix}\cosh\phi_1 & -\sinh\phi_1\cr -\sinh\phi_1 & \cos... ...n{pmatrix}\cosh\phi_2 & -\sinh\phi_2\cr -\sinh\phi_2 & \cosh\phi_2\end{pmatrix}$$

$$=\begin{pmatrix}\cosh\phi_1\cosh\phi_2 + \sinh\phi_1\sinh\phi_2 &... ...phi_2\sinh\phi_1 & \cosh\phi_1\cosh\phi_2 + \sinh\phi_1\sinh\phi_2\end{pmatrix}$$

$$=\begin{pmatrix}\cosh(\phi_1+\phi_2) & -\sinh(\phi_1+\phi_2)\cr -\sinh(\phi_1+\phi_2) & \cosh(\phi_1+\phi_2)\end{pmatrix}$$

$$=\mathbb{B}(\phi_1+\phi_2)$$

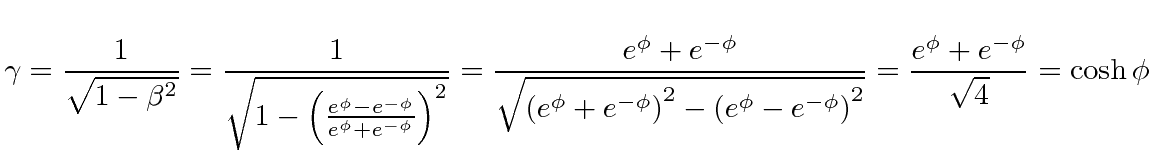
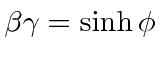
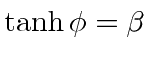
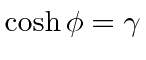
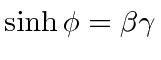
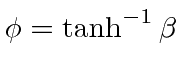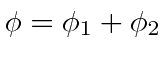
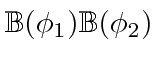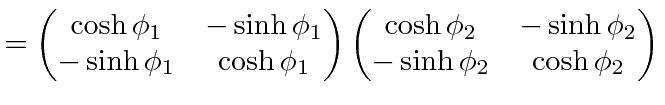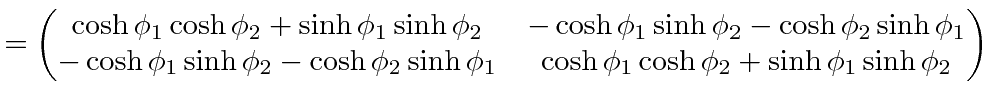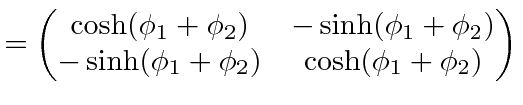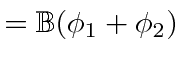This gives us our simplest calculation of the velocity addition formula.

$$\beta=\tanh(\phi_1+\phi_2)=\frac{\tanh\phi_1... ...}{1 + \tanh\phi_1 \tanh\phi_2} ={\beta_1+\beta_2\over 1+\beta_1\beta_2}$$

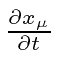This never becomes bigger than one and therefore no velocity can exceed the speed of light. The velocity addition formula can also be derived by considering the derivative of the position vector with respect to proper time, which is time in the rest frame. This derivative is a 4-vector while ${\partial x_\mu\over \partial t}$ is not a 4-vector.