Proper Time

For an object, a particle, or an observer, the invariant spacetime interval between two events for that object is never spacelike because the object cannot move faster than the speed of light.

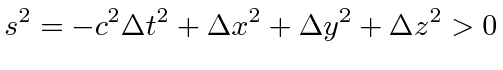
$\bgroup\color{black}$\displaystyle s^2=-c^2\Delta t^2+\Delta x^2+\Delta y^2+\Delta z^2 >0 $\egroup$

So the space time interval for an object can always be written as the time interval in the object's rest frame.

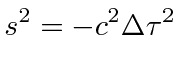
$\bgroup\color{black}$\displaystyle s^2=-c^2\Delta \tau^2 $\egroup$

So it is convenient to use the proper time $\bgroup\color{black}$ \tau$\egroup$ to understand the object's motion. $\bgroup\color{black}$ \tau$\egroup$ is a scalar quantity since it is directly related to the scalar spacetime interval.

As the length of a vector is the square root of the dot product of the vector with itself in Euclidean space, the proper time is essentially the square root of the dot product of a vector with itself in Minkowski space (up to the factor of $\bgroup\color{black}$ c$\egroup$ and the negative sign for timelike vectors that is conventional).

We will use the proper time to help us define the velocity and momentum in Minkowski space.

Jim Branson 2012-10-21