Minkowski Space

In 1907, Hermann Minkowski proposed that special relativity could be best expressed in a 4-dimensional geometry, with a new and unusual dot product. The fourth dimension would be time if we set $c=1$, but, we will continue with $ct$ as the fourth dimension, since we are stuck with the SI units of length and time for most real problems. This is not Euclidean 4-dimensional space but rather what has become known as Minkowski space.

Minkowski Space is a 4-dimensional real vector space, spanned by unit vectors with the property

$$\hat{e}_x^2=\hat{e}_y^2=\hat{e}_z^2=-\hat{e}_t^2=1.$$

We may number the coordinates like we have in three dimensions, with the time dimension getting the integer number 0. So that the 4-vector position would be.

$$x_\mu=(ct,x,t,z)$$

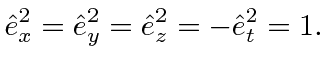
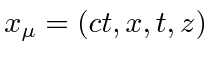
Note that we use Greek letters for the indices in 4-vectors. The Einstein summation convention was actually made for this. For example the ``dot product'' of a position vector with itself is

$$x_\mu x_\mu=-(ct)^2+x^2+y^2+z^2$$

As we noticed above for the muon decay, this dot product is invariant under Lorentz boosts. It is also invariant under rotations so we call it a scalar.

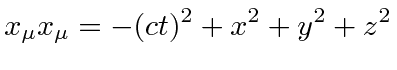
We may speak of a space-time coordinate like $x_\mu$ as an event, since to describe an event we need to know the location and the time, particularly if we need to transform it into another reference frame. We investigated the interval between the muon's production and decay in two inertial frames and found them to be equal.

$$s^2=-c^2\Delta t^2+\Delta x^2+\Delta y^2+\Delta z^2$$

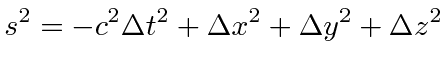
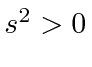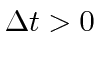This is an invariant quantity which can be used to classify the interval between two events to be spacelike for $s^2>0$, timelike for $s^2<0$ or lightlike for $s^2=0$. For timelike separations, an event can be in the future for $\Delta t>0$ or in the past for 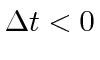$\Delta t<0$. If the separation is spacelike, the events are not causally connected in either direction. That is light from one event cannot get to the other.

Minkowski space seems to preserve causality. An event from the future cannot be transformed into the past or the present, even though the value of time can change under boosts.

The norm of a vector can be positive, negative or zero, making the vector spacelike, timelike, or lightlike respectively.

We do not perceive the world to be a 4 dimensional Minkowski space because we humans move much to slowly. We therefore move at very small angles from the time axis, and we make up our units so that velocities are 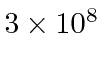$3\times 10^8$ bigger than they would be in natural units.