Checking Michelson Morley with Lorentz Transformation

Lets again look at MM in the frame in which the sun is at rest, now using the Lorentz Transformation. Light moves at the speed of light in every frame but the length parallel to motion is reduced ³. Starting in the parallel direction.

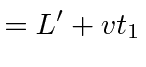$\displaystyle ct_1$	$\displaystyle = L'+vt_1$	time out to mirror
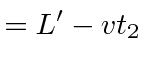$\displaystyle ct_2$	$\displaystyle =L'-vt_2$	time back
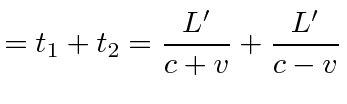$\displaystyle t$	$\displaystyle =t_1+t_2= {L'\over c+v}+{L'\over c-v}$
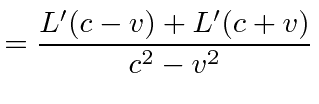	$\displaystyle ={L'(c-v)+L'(c+v)\over c^2-v^2}$
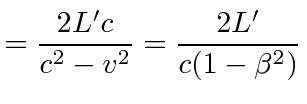	$\displaystyle ={2L'c\over c^2-v^2}={2L'\over c(1-\beta^2)}$
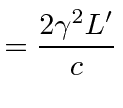$\displaystyle t_\parallel$	$\displaystyle ={2\gamma^2 L'\over c}$
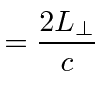$\displaystyle t$	$\displaystyle ={2L_\perp\over c}$
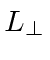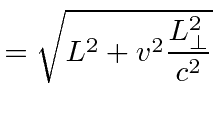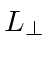$\displaystyle L_\perp$	$\displaystyle =\sqrt{L^2+v^2{L_\perp^2\over c^2}}$	$L_\perp$ not changed
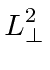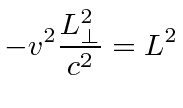$\displaystyle L_\perp^2$	$\displaystyle -v^2{L_\perp^2\over c^2}=L^2$
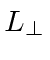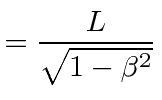$\displaystyle L_\perp$	$\displaystyle ={L\over \sqrt{1-\beta^2}}$
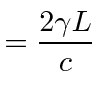$\displaystyle t_\perp$	$\displaystyle ={2\gamma L\over c}$
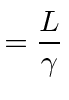$\displaystyle L'$	$\displaystyle ={L\over \gamma}$	Fitzgerald contraction
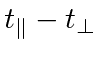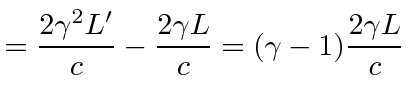$\displaystyle t_\parallel-t_\perp$	$\displaystyle ={2\gamma^2 L'\over c}-{2\gamma L\over c}=(\gamma-1){2\gamma L\over c}$	using transformed length
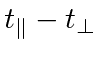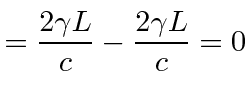$\displaystyle t_\parallel-t_\perp$	$\displaystyle ={2\gamma L\over c}-{2\gamma L\over c}=0$	no shift

Fitzgerald postulated that the length along the direction of motion changes as we transform to a moving frame. This is confirmed in the Lorentz transformation. With this transformation, the speed of light is the same in any frame and the Michelson-Morley experiment's null result is expected.