Next: The Lorentz Transformation Up: Special Relativity Previous: Some History of Special Contents
Lets discuss the Michelson Morley Experiment from two points of view.
First, assuming there is an ether which picks one frame in which the velocity of light is
![]() and
second, if the speed of light is the same in every frame.
In the first case, we want to see if the experiment would be sensitive to the motion of the earth through the ether.
In the second case we want to see what problems the constancy of the speed of light presents.
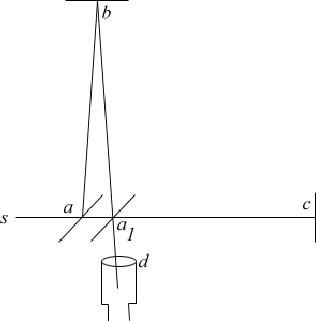
A diagram of the MM apparatus is show below.
and
second, if the speed of light is the same in every frame.
In the first case, we want to see if the experiment would be sensitive to the motion of the earth through the ether.
In the second case we want to see what problems the constancy of the speed of light presents.
A diagram of the MM apparatus is show below.
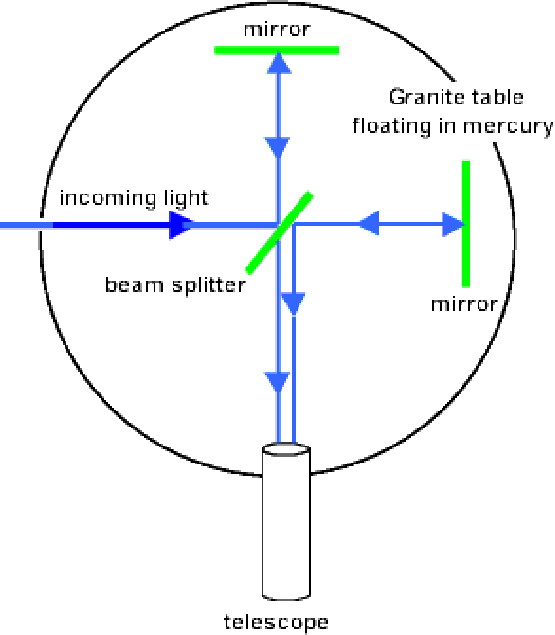
We will use some of the standard symbols of special relativity in this calculation.
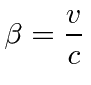
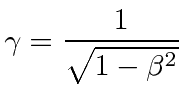
If the earth is moving through the ether at a velocity
![]() , and light moves at a velocity
, and light moves at a velocity
![]() through the medium of
the ether, then a careful calculation is needed.
In the
direction parallel to the velocity of the earth through the ether, the time taken for the round trip is.
through the medium of
the ether, then a careful calculation is needed.
In the
direction parallel to the velocity of the earth through the ether, the time taken for the round trip is.
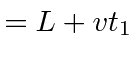 |
trip out to mirror | ||
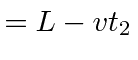 |
trip back to detector | ||
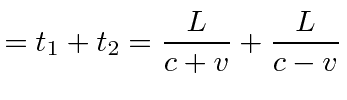 |
|||
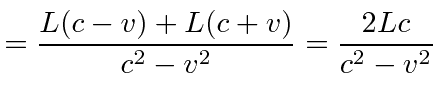 |
|||
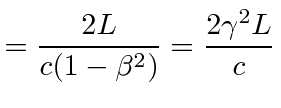 |
round trip time |
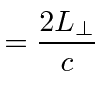 |
time for full trip |
||
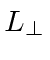 |
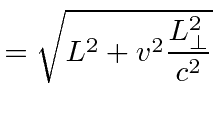 |
distance of |
|
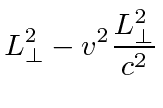 |
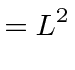 |
||
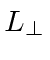 |
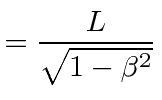 |
||
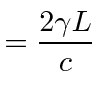 |
round trip time |
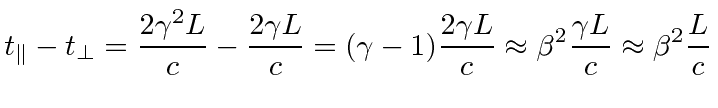
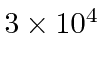 meters per second or about 10000 times smaller than the speed of light.
The
distance difference seen by the interferometer will be about.
meters per second or about 10000 times smaller than the speed of light.
The
distance difference seen by the interferometer will be about.
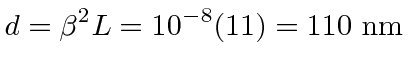
In the case that the laws of physics and the speed of light are the same in any frame, it is certainly easiest to compute what will happen in the rest frame of the experiment. In that frame, things are very simple.
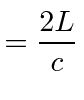 |
||
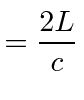 |
Lets look at it (with no relativity), for example, in the frame in which the sun is at rest, which is very much like the putative ether frame. Light moves at the speed of light in that frame and the calculation we had for the ether is correct, if we assume that the lengths are the same in that frame.
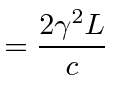 |
||
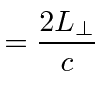 |
||
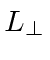 |
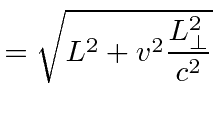 |
|
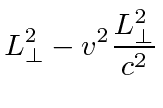 |
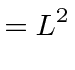 |
|
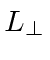 |
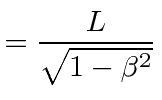 |
|
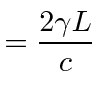 |
||
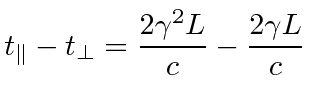 |
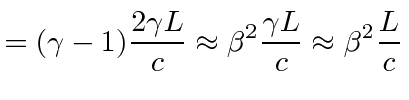 |
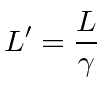
Jim Branson 2012-10-21