Next: Weather Systems Up: The Tides Previous: Example: Deflection of a Contents
People have been known to fire cannon balls in many direction and in many locations near the earth.
Let us consider the effect of the Coriolis force on the ballistic trajectories of these cannon balls.
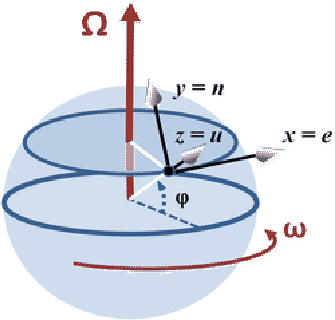
Assume the cannon ball is fired at an angle
![]() from the vertical and at and angle
from the vertical and at and angle
![]() from the easterly direction in the plane tangent to the earth.
These are the usual angles of a spherical coordinate system.
from the easterly direction in the plane tangent to the earth.
These are the usual angles of a spherical coordinate system.

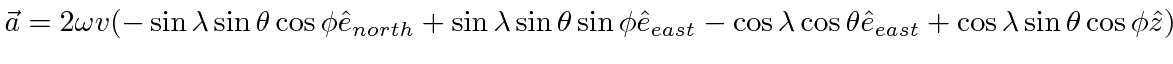
Jim Branson 2012-10-21