Next: Example: Deflection of Cannon Up: The Tides Previous: The Tides Contents
If we
drop an object from height
![]() , the effect of the centrifugal force is already in the
local value and local direction of
, the effect of the centrifugal force is already in the
local value and local direction of
![]() .
The Coriolis force is not included and it is proportional to velocity so it will not affect the direction
of plumb bobs.
The
Coriolis force will cause a deflection from a vertical path as the object falls.
Lets call the
.
The Coriolis force is not included and it is proportional to velocity so it will not affect the direction
of plumb bobs.
The
Coriolis force will cause a deflection from a vertical path as the object falls.
Lets call the
![]() direction the local upward vertical.
We need to pick two directions perpendicular to that to form a coordinate system.
We can choose the
direction the local upward vertical.
We need to pick two directions perpendicular to that to form a coordinate system.
We can choose the
![]() direction be be north and then we must choose east to be in the
direction be be north and then we must choose east to be in the
![]() direction to
have a right handed coordinate system.
direction to
have a right handed coordinate system.

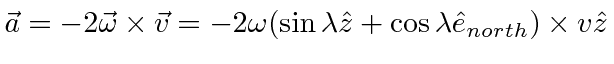
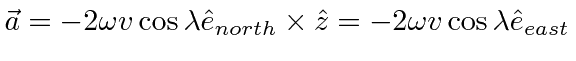
One can integrate this equation to find the deflection when a cannonball is dropped from a height
![]() .
.
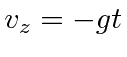 |
||
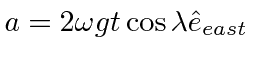 |
||
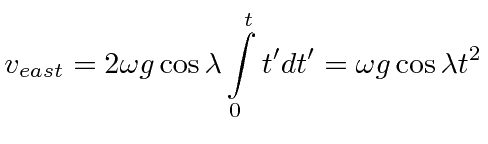 |
||
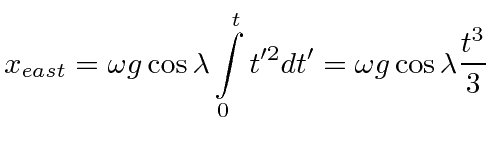 |
||
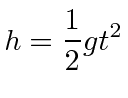 |
||
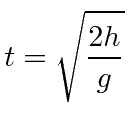 |
||
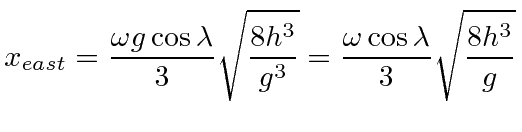 |
Jim Branson 2012-10-21