Next: Homework Up: Hamiltonian Mechanics Previous: Example: Motion in a Contents
An example of the theoretical utility of the Hamiltonian formalism is Liouville's Theorem. In Classical Mechanics, the complete state of a particle can be given by its coordinates and momenta. For example in three dimensions, there are three spatial coordinates and three conjugate momenta. If we consider a six dimensional phase space, a point in that space represents the state of a particle. A particle will follow a determined path through phase space, that is, given the particles full state (a point in phase space), our equations of motion will yield the phase space location of the particle at a later time (or even an earlier time). So particles follow determined paths through (six dimensional) phase space. (These paths do not intersect.)
Now
consider a large number of particles, perhaps in a beam.
These particles can be described by one point in phase space per particle.
For really large numbers of particles in a system, or if we consider a theoretical ensemble of particles,
the system can be
described as a density
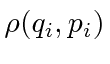 which is a function of the position in phase space.
which is a function of the position in phase space.
Liouville's Theorem states that the density of particles in phase space is a constant
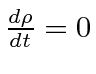 ,
so we wish to calculate the rate of change of the density of particles.
Imagine we shoot a burst of particles at the moon. The burst is localized in space and in momentum.
The burst moves toward the moon and so clearly the density near the earth is decreased, however,
the density we are interested in is essentially, the density around one of the particles, not the density at
some fixed point.
That is,
the point in phase space at which we wish to measure the density, moves with the particles.
The bunch of particles spreads out in coordinates space but the coordinate is highly correlated with the momentum so
the density in phase space can remain constant.
,
so we wish to calculate the rate of change of the density of particles.
Imagine we shoot a burst of particles at the moon. The burst is localized in space and in momentum.
The burst moves toward the moon and so clearly the density near the earth is decreased, however,
the density we are interested in is essentially, the density around one of the particles, not the density at
some fixed point.
That is,
the point in phase space at which we wish to measure the density, moves with the particles.
The bunch of particles spreads out in coordinates space but the coordinate is highly correlated with the momentum so
the density in phase space can remain constant.
To
``prove'' Liouville's theorem, we will calculate the rate of change of the number of particles in an
infinitesimal hypercube in phase space.
Consider the cube face perpendicular to
![]() for example.
The flow of particles through the face is
for example.
The flow of particles through the face is
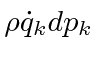 times all the other dimensions of the face
times all the other dimensions of the face
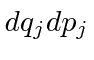 for
for
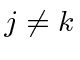 .
Then
the rate of change of the number of particles in the hypercube, due to flow through this face and the one opposite it is.
.
Then
the rate of change of the number of particles in the hypercube, due to flow through this face and the one opposite it is.
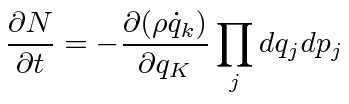
![\bgroup\color{black}$\displaystyle {\partial N\over \partial t}=-\sum\limits_k\l...
...al (\rho \dot{p}_k)\over \partial p_K}\right]\prod\limits_j dq_j dp_j . $\egroup](img1334.png)
![\bgroup\color{black}$\displaystyle {\partial \rho \over \partial t}=-\sum\limits...
...ver \partial q_K}
+{\partial (\rho \dot{p}_k)\over \partial p_K}\right] $\egroup](img1335.png)
![$\displaystyle ={\partial \rho \over \partial t}+\sum\limits_k\left[{\partial \r...
...over \partial q_K}\dot{q}_k +{\partial \rho \over \partial p_K}\dot{p}_k\right]$](img1337.png) |
||
![$\displaystyle =-\sum\limits_k\left[{\partial (\rho \dot{q}_k)\over \partial q_K...
...over \partial q_K}\dot{q}_k +{\partial \rho \over \partial p_K}\dot{p}_k\right]$](img1338.png) |
||
![$\displaystyle =\sum\limits_k\left[-{\partial \rho \over \partial q_K}\dot{q}_k-...
...over \partial q_K}\dot{q}_k +{\partial \rho \over \partial p_K}\dot{p}_k\right]$](img1339.png) |
||
![$\displaystyle =\sum\limits_k\left[-{\partial \dot{q}_k\over \partial q_K} -{\partial \dot{p}_k\over \partial p_K}\right]\rho$](img1340.png) |
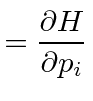 |
||
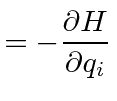 |
||
![$\displaystyle =\sum\limits_k\left[-{\partial^2 H\over \partial q_K\partial p_K} +{\partial^2 H\over \partial p_K\partial q_K}\right]\rho = 0$](img1341.png) |
Jim Branson 2012-10-21