Next: Phase Space and Liouville's Up: Hamiltonian Mechanics Previous: Example: A spherical pendulum Contents
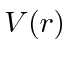
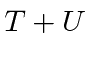 for this simple case if we don't choose coordinates that are time dependent.
Due to the spherical symmetry of the potential (and of the kinetic energy term),
the momentum conjugate to
for this simple case if we don't choose coordinates that are time dependent.
Due to the spherical symmetry of the potential (and of the kinetic energy term),
the momentum conjugate to
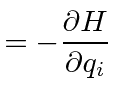 |
||
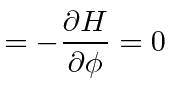 |
||
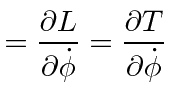 |
||
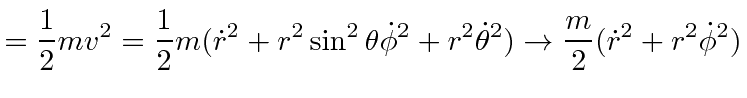 |
||
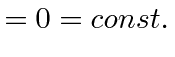 |
||
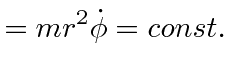 |
||
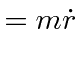 |
||
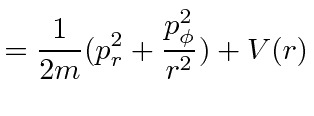 |
||
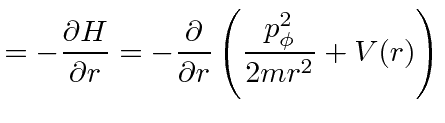 |
Jim Branson 2012-10-21