Next: About this document ... Up: Continuum Mechanics Previous: Continuum Mechanics Contents
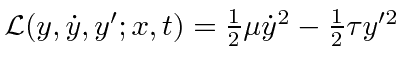 .
What is the momentum conjugate to the coordinate
.
What is the momentum conjugate to the coordinate 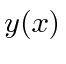 ?
Calculate the Hamiltonian density.
What is the Lagrange equation?
?
Calculate the Hamiltonian density.
What is the Lagrange equation?
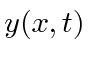 :
:
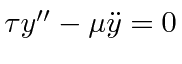 , into an equation for
, into an equation for
 where
where  and
and 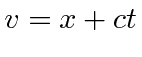 .
What should
.
What should  ?
?
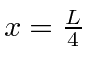 to a height
to a height 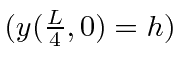 ,
with the rest of the string forming two lines meeting at that point, what is the formula for
,
with the rest of the string forming two lines meeting at that point, what is the formula for 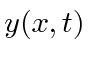 at a later time?
at a later time?