- A massless spring of unstretched length
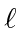 and spring constant
and spring constant 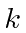 connects two masses
connects two masses 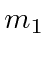 and
and 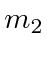 .
The system floats in space with no external forces.
Other than the spring connection, the two masses are free to move in any direction (6 coordinates).
Write the Lagrangian for the system.
Find as many conserved momenta as possible by choosing the best coordinates you can to describe the system.
Write Hamilton's equations of motion for this system.
.
The system floats in space with no external forces.
Other than the spring connection, the two masses are free to move in any direction (6 coordinates).
Write the Lagrangian for the system.
Find as many conserved momenta as possible by choosing the best coordinates you can to describe the system.
Write Hamilton's equations of motion for this system.
- A spherical pendulum consists of a bob of mass
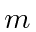 attached to a massless extensionless rod of length
attached to a massless extensionless rod of length 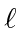 .
The other end of the rod is attached to a fixed frictionless pivot point.
Find the equation of motion using the Hamiltonian using the conserved momentum and to derive an effective potential.
Sketch the potential as a function of
.
The other end of the rod is attached to a fixed frictionless pivot point.
Find the equation of motion using the Hamiltonian using the conserved momentum and to derive an effective potential.
Sketch the potential as a function of 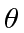 for several values of the momentum
for several values of the momentum 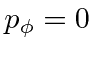 .
Under what conditions will the motion be at a constant
.
Under what conditions will the motion be at a constant 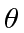 ?
?
- Consider a beam of electrons moving in the
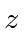 direction with constant intensity inside a circle of radius
direction with constant intensity inside a circle of radius 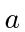 .
The beam is made to have only a small but important spread in transverse momentum.
Assume that the momentum is also of uniform density over a circle of radius
.
The beam is made to have only a small but important spread in transverse momentum.
Assume that the momentum is also of uniform density over a circle of radius 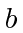 in momentum space.
Before the beam can spread out, a focusing element focuses the beam down to a circle of radius
in momentum space.
Before the beam can spread out, a focusing element focuses the beam down to a circle of radius  in the
in the 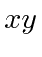 plane.
Assume that this a measured at the point where the radius is a minimum.
What will the distribution of transverse momenta be at the focus?
Draw a diagram of the motion of the particles which includes the region before the focusing element,
after it, and after the focus.
plane.
Assume that this a measured at the point where the radius is a minimum.
What will the distribution of transverse momenta be at the focus?
Draw a diagram of the motion of the particles which includes the region before the focusing element,
after it, and after the focus.
Jim Branson
2012-10-21
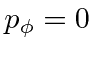 .
Under what conditions will the motion be at a constant
.
Under what conditions will the motion be at a constant  in the
in the